题目内容

抛物线y2=2px（p＞0）的焦点为F，焦点弦AB的倾斜角为30°，则
|AF|
|FB|
=
 
．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：求抛物线y2=2px的焦点，设直线l的方程与抛物线联立，求得xA，xB，利用抛物线定义，即可求得结论．
解答： 解：抛物线y2=2px的焦点F（
p
2
，0），
∵焦点弦AB的倾斜角为30°，
∴设直线l：y=
3
3
（x-
p
2
）与抛物线y2=2px联立，整理可得：x2-7px+
p2
4
=0，解得：
x=（
7
2
±2
3
 ）p，
由题设可得：xA=(
7
2
+2
3
)p，xB=(
7
2
-2
3
)p，
由抛物线定义可知：|AF|=xA+
p
2
=(4+2
3
)p，|BF|=xB+
p
2
=(4-2
3
)p，
∴
|AF|
|FB|
=
(4+2
3
)p
(4-2
3
)p
=7+4
3
，
则xA=(
7
2
-2
3
)p，xB=(
7
2
+2
3
)p时，
|AF|
|FB|
=7-4
3

故答案为：7±4
3
点评：本题考查抛物线的性质，考查直线与抛物线的位置关系，考查抛物线的定义，求得A，B的坐标是关键．
练习册系列答案
相关题目
设复数z1=1+i，z2=2+xi，（x∈R），若z1•z2∈R，则x的值等于
 
．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
5
3
，设其左、右焦点分别为F1，F2，上顶点为B1，且F2到直线B1F1的距离为
4
5
3
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点（2，0）作直线与椭圆交于A，B两点，O是坐标原点，是否存在这样的直线，使得|
OA
+
OB
|=|
OA
-
OB
|？若存在，求出直线的方程，若不存在，试说明理由．
已知函数f（x）=lnx+
1-x
a(1+x)
，其中a为不为零的常数．
（Ⅰ）若f（x）在点（1，0）处的切线过点（2，-1），求实数a的值；
（Ⅱ）当a=1时，若存在x1，x2∈[1，e2]使得f（x1）-f（x2）≥M成立，求满足条件的最大整数M；
（Ⅲ）若f（x）无极值，求实数a的取值范围．
在直角坐标系xOy中，以O为极点，X轴正半轴为极轴建立坐标系，直线l的极坐标方程为ρcos（θ-
π
3
）=
a-b
2
，与曲线C：ρ=
2
交于A，B两点，已知|AB|≥
6
．
（1）求直线l与曲线C的直角坐标方程；
（2）若动点P（a，b）在曲线C围成的区域内运动，求点P所表示的图形的面积．
已知圆C：x2+y2-6x+8y+21=0，动圆P的半径为5，且与圆C内切，则点P的轨迹方程为
 
．
如图，正四棱锥S-ABCD，底面边长与高都是2，K是SC的中点，T是SB的中点．
（1）求证：KT∥平面SAD；
（2）求二面角K-AD-B的大小的余弦值．
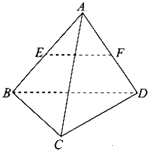如图，四面体ABCD的每条棱长都等于2，点E，F分别为棱AB，AD的中点，则|
AB
+
BC
|=
 
，|
BC
-
EF
|=
 
，
EF
与
AC
所成的角为
 
．
在平面直角坐标系xOy中，直线l的参数方程为
x=2+2t
y=1-t
（t为参数），椭圆C的方程为
x2
4
+y2=1，试在椭圆C上求一点P，使得P到直线l的距离最小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网