题目内容
已知椭圆
+
=1(a>b>0)的离心率为
,设其左、右焦点分别为F1,F2,上顶点为B1,且F2到直线B1F1的距离为
.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(2,0)作直线与椭圆交于A,B两点,O是坐标原点,是否存在这样的直线,使得|
+
|=|
-
|?若存在,求出直线的方程,若不存在,试说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 3 |
4
| ||
| 3 |
(Ⅰ)求椭圆的方程;
(Ⅱ)过点(2,0)作直线与椭圆交于A,B两点,O是坐标原点,是否存在这样的直线,使得|
| OA |
| OB |
| OA |
| OB |
考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)直线B1F1的方程为bx-cy+bc=0,由已知得
=
,
=
,由此能求出椭圆的方程.
(Ⅱ)由|
+
|=|
-
|,得:
•
=0,设直线的方程为y=k(x-2),由
,得(9k2+4)x2-36k2x+36(k2-1)=0,由此利用根的判别式、韦达定理,结合已知条件能求出满足条件的直线方程.
| 2bc |
| a |
4
| ||
| 3 |
| c |
| a |
| ||
| 3 |
(Ⅱ)由|
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
|
解答:
解:(Ⅰ)直线B1F1的方程为
+
=1,即bx-cy+bc=0,
由F2到直线B1F1的距离为
,得
=
=
,
又
=
,所以b=2,a=3,…(4分)
所以椭圆的方程为
+
=1.…(5分)
(Ⅱ)由|
+
|=|
-
|,得:
•
=0,
若直线的斜率不存在,直线的方程为x=2
由
,得
,
所以
•
=
与
•
=0矛盾,故直线的斜率存在,…(7分)
设直线的方程为y=k(x-2),由
,
得(9k2+4)x2-36k2x+36(k2-1)=0,
由题意△>0恒成立,设A(x1,y1),B(x2,y2),
则x1+x2=
,x1x2=
,…(9分)
由
•
=0,得x1x2+y1y2=0,
所以x1x2+y1y2=x1x2+k2(x1-2)(x2-2)=(1+k2)x1x2-2k2(x1+x2)+4k2=0,
把x1+x2=
,x1x2=
,
代入得(1+k2)•
-2k2•
+4k2,
解得k=±
,…(13分)
所以直线的方程为y=±
(x-2),
即3x-2y-6=0或3x+2y-6=0.…(14分)
| x |
| -c |
| y |
| b |
由F2到直线B1F1的距离为
4
| ||
| 3 |
| 2bc | ||
|
| 2bc |
| a |
4
| ||
| 3 |
又
| c |
| a |
| ||
| 3 |
所以椭圆的方程为
| x2 |
| 9 |
| y2 |
| 4 |
(Ⅱ)由|
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
若直线的斜率不存在,直线的方程为x=2
由
|
|
所以
| OA |
| OB |
| 16 |
| 9 |
| OA |
| OB |
设直线的方程为y=k(x-2),由
|
得(9k2+4)x2-36k2x+36(k2-1)=0,
由题意△>0恒成立,设A(x1,y1),B(x2,y2),
则x1+x2=
| 36k2 |
| 9k2+4 |
| 36(k2-1) |
| 9k2+4 |
由
| OA |
| OB |
所以x1x2+y1y2=x1x2+k2(x1-2)(x2-2)=(1+k2)x1x2-2k2(x1+x2)+4k2=0,
把x1+x2=
| 36k2 |
| 9k2+4 |
| 36(k2-1) |
| 9k2+4 |
代入得(1+k2)•
| 36(k2-1) |
| 9k2+4 |
| 36k2 |
| 9k2+4 |
解得k=±
| 3 |
| 2 |
所以直线的方程为y=±
| 3 |
| 2 |
即3x-2y-6=0或3x+2y-6=0.…(14分)
点评:本题考查椭圆方程的求法,考查满足条件的直线是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
| ∫ |
-π |
| A、0 | B、1 | C、2 | D、3 |
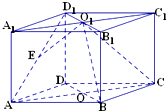 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC与BD交于点O,A1C1与B1D1交于点O1,E为AD1的中点.