题目内容
 如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.
如图,正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点.(1)求证:KT∥平面SAD;
(2)求二面角K-AD-B的大小的余弦值.
考点:用空间向量求平面间的夹角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)由已知得KT∥BC,BC∥AD,从而KT∥AD,由此能证明KT∥平面SAD.
(2)以O为原点,OA为x轴,OB为y轴,以OS为z轴,建立空间直角坐标系,由此利用向量法能求出二面角K-AD-B的余弦值.
(2)以O为原点,OA为x轴,OB为y轴,以OS为z轴,建立空间直角坐标系,由此利用向量法能求出二面角K-AD-B的余弦值.
解答:
(1)证明:∵正四棱锥S-ABCD,底面边长与高都是2,K是SC的中点,T是SB的中点,
∴KT∥BC,BC∥AD,
∴KT∥AD,
∵KT?平面SAD,AD?平面SAD,
∴KT∥平面SAD.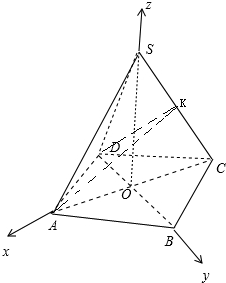
(2)解:以O为原点,OA为x轴,OB为y轴,以OS为z轴,
建立空间直角坐标系,
A(
,0,0),B(0,
,0),D(0,-
,0),
S(0,0,2),C(-
,0,0),K(-
,0,1),
=(
,
,0),
=(-
,
,1),
设平面DAK的法向量
=(x,y,z),
,
取x=1,得
=(1,-1,
),
又平面ADB的法向量
=(0,0,1),
设二面角K-AD-B的大小的平面角为θ,
cosθ=|cos<
,
>|=|
|=
.
∴KT∥BC,BC∥AD,
∴KT∥AD,
∵KT?平面SAD,AD?平面SAD,
∴KT∥平面SAD.

(2)解:以O为原点,OA为x轴,OB为y轴,以OS为z轴,
建立空间直角坐标系,
A(
| 2 |
| 2 |
| 2 |
S(0,0,2),C(-
| 2 |
| ||
| 2 |
| DA |
| 2 |
| 2 |
| DK |
| ||
| 2 |
| 2 |
设平面DAK的法向量
| n |
|
取x=1,得
| n |
3
| ||
| 2 |
又平面ADB的法向量
| m |
设二面角K-AD-B的大小的平面角为θ,
cosθ=|cos<
| m |
| n |
| ||||
|
3
| ||
| 13 |
点评:本题考查直线与平面平行的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目