题目内容
设数列{an}的前n项和为Sn，满足2Sn=an+1-2n+1+1，n∈N*，且a1=1．
（1）求数列{an}的通项公式；
（2）求数列{
}的前n项和Tn．
（1）求数列{an}的通项公式；
（2）求数列{
| nan |
| 3n |
考点：数列的求和,数列递推式
专题：点列、递归数列与数学归纳法
分析：（1）根据条件，建立方程组，构造等比数列即可求数列{an}的通项公式；
（2）利用错位相减法以及分组求和法即可求数列{
}的前n项和Tn．
（2）利用错位相减法以及分组求和法即可求数列{
| nan |
| 3n |
解答：
解：（1）∵2Sn=an+1-2n+1+1，
∴2Sn-1=an-2n+1，（n≥2），
两式相减得2（Sn-Sn-1）=an+1-an-2n+1+2n，
即2an=an+1-an-2n，则an+1=3an+2n，
整理得an+1+2n+1=3（an+2n），
即{an+2n}是首项为a1+2=1+2=3，公比q=3的等比数列，
则an+2n=3•3n-1=3n，
则an=3n-2n，即数列数列{an}的通项公式为an=3n-2n．
（2）∵an=3n-2n，∴
=
=n（1-（
）n）=n-n•（
）n，
设数列{n•（
）n}的前n项和为Sn，
则Sn=1•（
）1+2•（
）2+…+n•（
）n，
Sn=1•（
）2+2•（
）3+…+n•（
）n+1，
两式相减得
Sn=1•（
）1+（
）2+…+（
）n-n•（
）n+1=
-n•（
）n+1
=2-2•（
）n-n•（
）n+1，
则Sn=6-6•（
）n-3n•（
）n+1=6-（6+2n）•（
）n，
则数列{
}的前n项和Tn=Sn+1+2+…+n=6-（6+2n）•（
）n+
．
∴2Sn-1=an-2n+1，（n≥2），
两式相减得2（Sn-Sn-1）=an+1-an-2n+1+2n，
即2an=an+1-an-2n，则an+1=3an+2n，
整理得an+1+2n+1=3（an+2n），
即{an+2n}是首项为a1+2=1+2=3，公比q=3的等比数列，
则an+2n=3•3n-1=3n，
则an=3n-2n，即数列数列{an}的通项公式为an=3n-2n．
（2）∵an=3n-2n，∴
| nan |
| 3n |
| n(3n-2n) |
| 3n |
| 2 |
| 3 |
| 2 |
| 3 |
设数列{n•（
| 2 |
| 3 |
则Sn=1•（
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
两式相减得
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| ||||
1-
|
| 2 |
| 3 |
=2-2•（
| 2 |
| 3 |
| 2 |
| 3 |
则Sn=6-6•（
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
则数列{
| nan |
| 3n |
| 2 |
| 3 |
| n(n+1) |
| 2 |
点评：本题主要考查数列的通项公式以及数列前n项和的计算，利用分组求和法以及错位相减法是解决本题的关键．综合性较强，运算量较大．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=x3+3x2+3x的单调增区间为（ ）
| A、（-∞，+∞） |
| B、（-∞，-1） |
| C、（0，+∞） |
| D、（-1，+∞） |
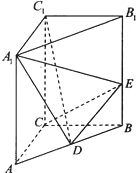
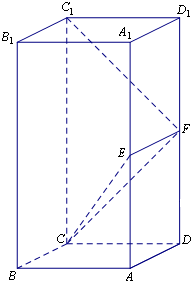在长方体ABCD-A1B1C1D1中，AA1=2AB，E，F分别是AA1，DD1的中点．