Question

三棱柱ABC-A₁B₁C₁中，AA₁=AC=BC=2，B₁E=BE，∠A₁DE=90°，∠ACB=90°，求证：A₁D⊥CD．

Answer 1

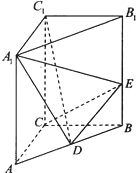
考点：空间中直线与直线之间的位置关系,棱柱的结构特征

专题：空间位置关系与距离

分析：由已知条件推导出CD⊥AB，AA₁⊥CD，从而得到CD⊥面A₁ABB₁，由此能证明A₁D⊥CD．

解答： 证明：连结AE，在△ABC中，∵AC=BC=2，∠ACB=90°，
∴AB=

4+4

=2

2

，
在△A₁B₁E中，∵直三棱柱ABC-A₁B₁C₁中AA₁=AC=BC=2，B₁E=BE，
∴A1E=

8+1

=3，
在△AA₁D中，A1D2=AA12+AD2，
在△BDE中，DE²=BE²+BD²，
在△A₁DE中，AE2=A1D2+DE2=AA₁²+AD²+BE²+BD²，
∵AB=AD+BD，∴AD=BD=

2

，
∴D是AB中点，∴CD⊥AB，
又在直三棱柱ABC-A₁B₁C₁中，
AA₁⊥底面ABC，∴AA₁⊥CD，
∴CD⊥面A₁ABB₁，
∵A₁D?面A₁ABB₁，∴A₁D⊥CD．

点评：本题考查异面直线垂直的证明，是中档题，解题时要认真审题，注意空间思维能力的培养．