题目内容
6.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0.b>0),若矩形ABCD的四个顶点在E上,AB,CD的中点为双曲线E的两个焦点,且双曲线E的离心率是2.直线AC的斜率为k.则|k|等于( )| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{5}{2}$ | D. | 3 |
分析 可令x=c,代入双曲线的方程,求得y=±$\frac{{b}^{2}}{a}$,再由题意设出A,B,C,D的坐标,由离心率公式,可得a,b,c的关系,运用直线的斜率公式,计算即可得到所求值.
解答 解:令x=c,代入双曲线的方程可得y=±b$\sqrt{\frac{{c}^{2}}{{a}^{2}}-1}$=±$\frac{{b}^{2}}{a}$,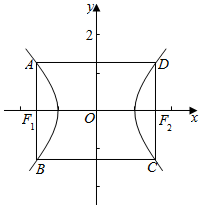
由题意可设A(-c,$\frac{{b}^{2}}{a}$),B(-c,-$\frac{{b}^{2}}{a}$),
C(c,-$\frac{{b}^{2}}{a}$),D(c,$\frac{{b}^{2}}{a}$),
由双曲线E的离心率是2,可得e=$\frac{c}{a}$=2,
即c=2a,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,
直线AC的斜率为k=$\frac{\frac{2{b}^{2}}{a}}{-2c}$=-$\frac{{b}^{2}}{ac}$=-$\frac{3{a}^{2}}{2{a}^{2}}$=-$\frac{3}{2}$.
即有|k|=$\frac{3}{2}$.
故选:B.
点评 本题考查双曲线的离心率的求法,注意运用方程的思想,正确设出A,B,C,D的坐标是解题的关键,考查运算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.已知$\frac{\overline z}{1+i}=2+i$,则复数z=( )
| A. | 1-3i | B. | -1-3i | C. | -1+3i | D. | 1+3i |
17.执行如图所示的程序框图,则输出的x等于( )


| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
1.对函数f(x)=$\left\{\begin{array}{l}{-x+1,x>0}\\{-x-1,x≤0}\end{array}\right.$性质,下列叙述正确为( )
| A. | 奇函数 | B. | 减函数 | ||
| C. | 既是奇函数又是减函数 | D. | 不是奇函数也不是减函数 |
11.已知函数f(x)=2sin(2x-$\frac{π}{6}$)+a,a为常数
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
(1)求函数f(x)的最小正周期;
(2)若x∈[0,$\frac{π}{2}$]时,f(x)的最小值为-2,求a的值.
18.在一段时间内,某种商品的价格x(元)和需求量y(件)之间的一组数据如表所示:
(1)求出y关于x的线性回归方程;
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
| 价格x/元 | 14 | 16 | 18 | 20 | 22 |
| 需求量y/件 | 56 | 50 | 3 | 1 | 37 |
(2)请用R2和残差图说明回归方程拟合效果的好坏.
参考数据:回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$中,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n(\overline{x})^{2}}$,$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x,R2=1-$\frac{\sum_{i=1}^{n}({y}_{i}-\widehat{{y}_{i}})^{2}}{\sum_{i=1}^{n}({y}_{i}-\overline{y})^{2}}$
参考数据:$\sum_{i=1}^5{x_i^2=1660}$,$\sum_{i=1}^5{{x_i}{y_i}}$=3992.
15.过正三棱柱底面一边所作的正三棱柱的截面是( )
| A. | 三角形 | B. | 三角形或梯形 | ||
| C. | 不是梯形的四边形 | D. | 梯形 |
16.同学聚会上,某同学从《爱你一万年》,《十年》,《父亲》,《单身情歌》四首歌选出两首歌进行表演,则《爱你一万年》未选取的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{5}{6}$ |