题目内容

1．对函数f（x）=$\left\{\begin{array}{l}{-x+1，x＞0}\\{-x-1，x≤0}\end{array}\right.$性质，下列叙述正确为（　　）
A．奇函数B．减函数
C．既是奇函数又是减函数D．不是奇函数也不是减函数

分析 奇函数在原点有定义时，f（0）=0，而本题f（0）=-1，且f（1）=0，从而得出f（x）不是奇函数，并且也不是减函数．

解答 解：f（0）=-1，f（1）=0；
∴f（x）不是奇函数也不是减函数．
故选D．

点评 考查奇函数、减函数的定义，奇函数f（x）在原点有定义时，满足f（0）=0．

练习册系列答案
相关题目
11．已知函数f（x）=|lnx|，g（x）=k（x-1）（k∈R）．
（1）若两个实数a，b满足0＜a＜b，且f（a）=f（b），求4a-b的取值范围；
（2）证明：当k＜1时，存在x0＞1，使得对任意的x∈（1，x0），恒有f（x）＞g（x）；
（3）已知0＜a＜b，证明：存在x0∈（a，b），使得$\frac{lnb-lna}{b-a}=\frac{1}{x_0}$．
12．在四棱锥P-ABCD中，PA⊥底面ABCD，底面ABCD是直角梯形，BA⊥AD，AD∥BC，AB=2，BC=1，PA=AD=3，E是PD上一点，且CE∥平面PAB，则C到面ABE的距离为$\frac{{2\sqrt{5}}}{5}$．
9．已知函数f（x）=$\frac{{2}^{x}-1}{{2}^{x}+1}$．
（1）求f[f（0）+4]的值；
（2）求证：f（x）在R上是增函数．
16．执行如图所示的程序框图，则输出的b值等于（　　）
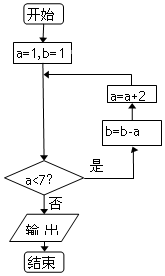
A．-24B．-15C．-8D．-3
6．已知双曲线E：$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0．b＞0），若矩形ABCD的四个顶点在E上，AB，CD的中点为双曲线E的两个焦点，且双曲线E的离心率是2．直线AC的斜率为k．则|k|等于（　　）
A．2B．$\frac{3}{2}$C．$\frac{5}{2}$D．3
13．已知a∈R，函数$f（x）=-\frac{1}{3}{x^3}+\frac{1}{2}a{x^2}+2ax（{x∈R}）$．
（1）当a=1时，求函数f（x）的单调递增区间；
（2）若函数f（x）在R上单调递减，求a的取值范围．
10．把十进制数93化为二进制数为1011101（2）．
11．已知数列{an}满足a1=-40，且nan+1-（n+1）an=2n2+2n，则an取最小值时n的值为10或11．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网