题目内容
若不等式x2+3x＞ax-4对于满足0≤x≤1的实数x恒成立，则实数a的取值范围是 ．
考点：二次函数的性质
专题：函数的性质及应用,导数的综合应用
分析：x=0时容易得到对于a∈R满足原不等式成立，x≠0时，即0＜x≤1，由原不等式得a＜x+
+3，令f（x）=x+
+3，通过求f′（x），根据f′（x）的符号可判断出函数在（0，1]上是减函数，所以f（1）=8是f（x）的最小值，所以a＜8．
| 4 |
| x |
| 4 |
| x |
解答：
解：①x=0时，原不等式变成0＞-4，该不等式成立，此时a∈R；
②x≠0时，由原不等式得：a＜x+
+3；
(x+
+3)′=1-
=
，∵0＜x≤1，∴x2-4＜0，(x+
+3)′＜0；
∴函数x+
+3在（0，1]上单调递减，所以x=1时，该函数在（0，1]上取最小值8；
∴a＜8；
综上得a的取值范围是（-∞，8）．
故答案为：（-∞，8）．
②x≠0时，由原不等式得：a＜x+
| 4 |
| x |
(x+
| 4 |
| x |
| 4 |
| x2 |
| x2-4 |
| x2 |
| 4 |
| x |
∴函数x+
| 4 |
| x |
∴a＜8；
综上得a的取值范围是（-∞，8）．
故答案为：（-∞，8）．
点评：考查函数导数符号和函数单调性的关系，根据函数单调性求函数的最小值．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
数列{an}中，若an+1=
，a1=1，则a2010=（ ）
| an |
| 2an+1 |
| A、4019 | ||
B、
| ||
| C、4021 | ||
D、
|
如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°，平面PAD⊥底面ABCD，Q为AD中点，M是棱PC上的点，PD=PA=2，BC=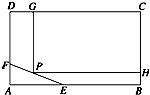
如图，长方形ABCD形状的空地，AB=100m，BC=80m，现决定在该空地上规划出一块矩形CGPH地面学生公寓，要求一边落在CD 上，但不得越过文物保护区△AEF的EF．△AEF的边AE=30m，AF=20m．