题目内容
下列说法中:
①函数y=lg(x2-ax-a)的值域为R,则a∈(-4,0);
②O是△ABC所在平面上一定点,动点P满足
=
+λ(
+
)且λ∈[0,+∞),则P的轨迹一定经过△ABC的重心;
③△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bcosB,则△ABC是等腰三角形;
④若函数f(x)=x+log2(x+
),则“m+n≥0”是“f(m)+f(n)≥0”的充要条件.其中所有正确命题的序号是 .
①函数y=lg(x2-ax-a)的值域为R,则a∈(-4,0);
②O是△ABC所在平面上一定点,动点P满足
| OP |
| OA |
| AB |
| AC |
③△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bcosB,则△ABC是等腰三角形;
④若函数f(x)=x+log2(x+
| x2+1 |
考点:命题的真假判断与应用
专题:函数的性质及应用,解三角形,平面向量及应用
分析:①,依题意知,y=x2-ax-a与x轴有公共点,由△=(-a)2-4×1×(-a)≥0,可判断①;
②,设BC中点为D,易知A、P、D三点共线,从而可判断②;
③,利用正弦定理与二倍角的正弦可得sin2A=sin2B,分析得到A=B或A+B=
,从而可判断③;
④可判断函数f(x)=x+log2(x+
)为R上的单调递增的奇函数,利用充分必要条件的概念可判断④.
②,设BC中点为D,易知A、P、D三点共线,从而可判断②;
③,利用正弦定理与二倍角的正弦可得sin2A=sin2B,分析得到A=B或A+B=
| π |
| 2 |
④可判断函数f(x)=x+log2(x+
| x2+1 |
解答:
解:对于①,函数y=lg(x2-ax-a)的值域为R,则y=x2-ax-a与x轴有公共点,故△=(-a)2-4×1×(-a)≥0,解得a∈[0,4],故①错误;
对于②,设BC中点为D,则AD为△ABC中BC边上的中线且
+
=2
,
∵
=
+λ(
+
),
∴
=
+λ(
+
),
∴
-
=λ(
+
),即
=λ(
+
)=2λ
,
∴AP∥AD,
∴A、P、D三点共线
所以点P一定过△ABC的重心,②正确.
对于③,△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bcosB,则sin2A=sin2B,
所以,2A=2B或2A=π-2B,即A=B或A+B=
,
故△ABC是等腰三角形或直角三角形,③错误;
对于④,因为f(x)=x+log2(x+
),其定义域为R,
所以f(-x)+f(x)=-x+log2(-x+
)+x+log2(x+
)=log2[(x+
)(-x+
)]=log21=0,
所以,f(-x)=-f(x),f(x)=x+log2(x+
)是奇函数,
由于函数y=x+
在区间[0,+∞)上是增函数,所以f(x)=x+log2(x+
)在区间[0,+∞)上是增函数,而f(x)=x+log2(x+
)是R上的奇函数,
故在R上单调递增;
所以,m+n≥0,即m≥-n时,f(m)≥f(-n)=-f(n),所以f(m)+f(n)≥0,即充分性成立;
反之,若f(m)+f(n)≥0,则f(m)≥-f(n)=f(-n),所以m≥-n,即m+n≥0,必要性成立;
所以“m+n≥0”是“f(m)+f(n)≥0”的充要条件,④正确.
故答案为:②④.
对于②,设BC中点为D,则AD为△ABC中BC边上的中线且
| AB |
| AC |
| AD |
∵
| OP |
| OA |
| AB |
| AC |
∴
| OP |
| OA |
| AB |
| AC |
∴
| OP |
| OA |
| AB |
| AC |
| AP |
| AB |
| AC |
| AD |
∴AP∥AD,
∴A、P、D三点共线
所以点P一定过△ABC的重心,②正确.
对于③,△ABC中,角A,B,C所对的边分别为a,b,c,若acosA=bcosB,则sin2A=sin2B,
所以,2A=2B或2A=π-2B,即A=B或A+B=
| π |
| 2 |
故△ABC是等腰三角形或直角三角形,③错误;
对于④,因为f(x)=x+log2(x+
| x2+1 |
所以f(-x)+f(x)=-x+log2(-x+
| x2+1 |
| x2+1 |
| x2+1 |
| x2+1 |
所以,f(-x)=-f(x),f(x)=x+log2(x+
| x2+1 |
由于函数y=x+
| x2+1 |
| x2+1 |
| x2+1 |
故在R上单调递增;
所以,m+n≥0,即m≥-n时,f(m)≥f(-n)=-f(n),所以f(m)+f(n)≥0,即充分性成立;
反之,若f(m)+f(n)≥0,则f(m)≥-f(n)=f(-n),所以m≥-n,即m+n≥0,必要性成立;
所以“m+n≥0”是“f(m)+f(n)≥0”的充要条件,④正确.
故答案为:②④.
点评:本题考查对数函数的值域,平面向量共线定理的应用,考查函数的奇偶性、单调性的综合应用,考查充分必要条件的判断,突出考查综合运用知识、解决问题的能力及钻研精神,属于难题.

练习册系列答案
相关题目
已知x、y满足(x-1)2+y2=1,则S=x2+y2+2x-2y+2的最小值是( )
A、6-2
| ||
B、
| ||
C、
| ||
| D、2 |
 如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.
如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.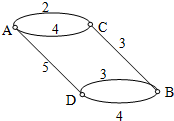 如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )
如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )