题目内容
解关于x的不等式:|x+2|-|2x-5|>a+1.
考点:绝对值不等式
专题:不等式的解法及应用
分析:设f(x)=|x+2|-|2x-5|=
,显然f(x)的最大值为f(
)=
,且f(-2)=-9.再分当a+1≥
、当-9<a+1<
时、当a+1≤-9时三种情况,分别根据f(x)的图象在直线y=a+1的上方,求出x的范围.
|
| 5 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
解答:
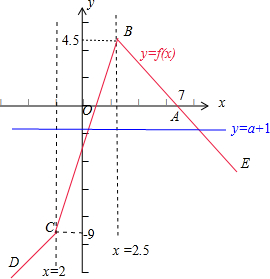 解:设f(x)=|x+2|-|2x-5|=
解:设f(x)=|x+2|-|2x-5|=
,
显然f(x)的最大值为f(
)=
,且f(-2)=-9.
由题意可得,函数f(x)的图象应该在直线y=a+1的上方.
当a+1≥
,即a≥
时,不等式无解;
当-9<a+1<
时,即-10<a<
时,由3x-3=a+1,求得x=
;由7-x=a+1,求得x=6-a,
故不等式解集为(
,6-a);
当a+1≤-9时,即a≤-10时,由x-7=a+1,求得x=8+a;由7-x=a+1,求得x=6-a,
故不等式解集为[a+8,6-a].
 解:设f(x)=|x+2|-|2x-5|=
解:设f(x)=|x+2|-|2x-5|=
|
显然f(x)的最大值为f(
| 5 |
| 2 |
| 9 |
| 2 |
由题意可得,函数f(x)的图象应该在直线y=a+1的上方.
当a+1≥
| 9 |
| 2 |
| 7 |
| 2 |
当-9<a+1<
| 9 |
| 2 |
| 7 |
| 2 |
| a+4 |
| 3 |
故不等式解集为(
| a+4 |
| 3 |
当a+1≤-9时,即a≤-10时,由x-7=a+1,求得x=8+a;由7-x=a+1,求得x=6-a,
故不等式解集为[a+8,6-a].
点评:本题主要考查绝对值不等式的解法,体现了数形结合、分类讨论、转化的数学思想,属于中档题.

练习册系列答案
相关题目
已知A={x|x≤1或x≥2},B={x|x>a},若A∪B=R,则实数a的取值范围是( )
| A、a≥1 | B、a>1 |
| C、a≤1 | D、a<1 |
 如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.
如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.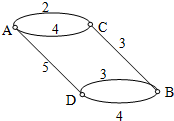 如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )
如图,小圆圈表示网络的接点,接点之间的连接表示它们有网线相连.相连标注的数字表示该段网线单位时间内可以通过的最大信息量.现在从接点A向接点B传递信息,信息可以分开沿不同线路同时传递,则单位时间内从接点A向接点B传递的最大信息量为( )