题目内容
 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD中点,M是棱PC上的点,PD=PA=2,BC=| 1 |
| 2 |
| 3 |
(1)若点M是棱PC的中点,求证:PA∥平面BMQ;
(2)求证:平面PQB⊥底面PAD;
(3)(仅理科做)若PM=3MC,求二面角M-BQ-C的大小.
考点:二面角的平面角及求法,直线与平面平行的判定,平面与平面垂直的判定
专题:综合题,空间位置关系与距离,空间角
分析:(1)本小题是一个证明线面平行的题,一般借助线面平行的判定定理求解,如图连接AC,交BQ于N,连接MN,先证明MN∥PA,再由线面平行的判定理证明线面平行;
(2)本小题是一个证明面面垂直的题,可采用面面垂直的定义求二面角是直角,或者用面面垂直的判定理证明,由题设条件知,利用面面垂直的判定定理证明较易,观察图形与题设条件,法一:可通过证明BQ⊥平面PAD来证明面面垂直;
(3)连结BD,以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系,求出平面BMQ和BCQ的法向量,代入向量夹角公式,可得答案.
(2)本小题是一个证明面面垂直的题,可采用面面垂直的定义求二面角是直角,或者用面面垂直的判定理证明,由题设条件知,利用面面垂直的判定定理证明较易,观察图形与题设条件,法一:可通过证明BQ⊥平面PAD来证明面面垂直;
(3)连结BD,以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系,求出平面BMQ和BCQ的法向量,代入向量夹角公式,可得答案.
解答:
解:(1)连接AC,交BQ于N,连接MN. …(1分)
∵BC∥AD且BC=
AD,即BC平行且等于AQ,
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M在是棱PC的中点,
∴MN∥PA.…(2分)
∵MN?平面MQB,PA?平面MQB,…(3分)
∴PA∥平面MBQ. …(4分)
(2)∵AD∥BC,BC=
AD,Q为AD的中点,
∴四边形BCDQ为平行四边形,∴CD∥BQ.…(6分)
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,…(7分)
∴BQ⊥平面PAD. …(8分)
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(9分)
(3)连结BD,∵底面ABCD是菱形,且∠BAD=60°,
∴△BAD是等边三角形,
∴BQ⊥AD由(Ⅰ)PQ⊥平面ABCD.
∴PQ⊥AD.
以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系
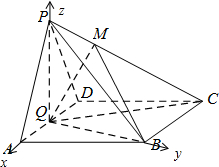
则Q(0,0,0),A(1,0,0),B(0,
,0),P(0,0,
).
设平面BMQ的法向量
=(x,y,z)为,
注意到MN∥PA,∴
,
解得
=(
,0,1)是平面BMQ的一个法向量
又∵平面BCQ的法向量为
=
=(0,0,
)
故二面角M-BQ-C的平面角θ满足:cosθ=
=
,
故θ=
,
即二面角M-BQ-C的平面角为
.…(12分)
∵BC∥AD且BC=
| 1 |
| 2 |
∴四边形BCQA为平行四边形,且N为AC中点,
又∵点M在是棱PC的中点,
∴MN∥PA.…(2分)
∵MN?平面MQB,PA?平面MQB,…(3分)
∴PA∥平面MBQ. …(4分)
(2)∵AD∥BC,BC=
| 1 |
| 2 |
∴四边形BCDQ为平行四边形,∴CD∥BQ.…(6分)
∵∠ADC=90°∴∠AQB=90° 即QB⊥AD.
又∵平面PAD⊥平面ABCD
且平面PAD∩平面ABCD=AD,…(7分)
∴BQ⊥平面PAD. …(8分)
∵BQ?平面PQB,
∴平面PQB⊥平面PAD. …(9分)
(3)连结BD,∵底面ABCD是菱形,且∠BAD=60°,
∴△BAD是等边三角形,
∴BQ⊥AD由(Ⅰ)PQ⊥平面ABCD.
∴PQ⊥AD.
以Q为坐标原点,QA,QB,QP分别为x轴y轴z轴建立空间直角坐标系

则Q(0,0,0),A(1,0,0),B(0,
| 3 |
| 3 |
设平面BMQ的法向量
| m |
注意到MN∥PA,∴
|
解得
| m |
| 3 |
又∵平面BCQ的法向量为
| n |
| QP |
| 3 |
故二面角M-BQ-C的平面角θ满足:cosθ=
|
| ||||
|
|
| 1 |
| 2 |
故θ=
| π |
| 3 |
即二面角M-BQ-C的平面角为
| π |
| 3 |
点评:本题考查面面垂直的证明方法以及线面平行的证明,考查面面角,解题的关键是利用线面平行的判定,理解面面角的定义,属于中档题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
已知x、y满足(x-1)2+y2=1,则S=x2+y2+2x-2y+2的最小值是( )
A、6-2
| ||
B、
| ||
C、
| ||
| D、2 |
 如图在边长为1正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz,
如图在边长为1正方体ABCD-A1B1C1D1中,以正方体的三条棱所在直线为轴建立空间直角坐标系Oxyz, 如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.
如图,四边形ABCD是正方形,MA⊥平面ABCD,MA∥PB,PB=AB=2MA=2.