题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{2x-4,0≤x<4}\\{lo{g}_{2}(x-2)+2,4≤x≤6}\end{array}\right.$,若存在x1,x2∈R,当0≤x1<4≤x2≤6时,f(x1)=f(x2),则x1f(x2)的取值范围是[$\frac{21}{2}$,16).分析 先求出x1的范围,再将x1f(x2)转化为x的函数,利用函数的单调性确定x1f(x2)的取值范围.
解答 解:∵存在x1,x2∈R,当0≤x1<4≤x2≤6时,f(x1)=f(x2),
∴log2(4-2)+2=3,log2(6-2)+2=4,
∴3≤2x1-4<4,
∴$\frac{7}{2}$≤x1<4
∵f(x1)=2x1-4,f(x1)=f(x2)
∴x1f(x2)=x1f(x1)=x1(2x1-4)=2x12-4x1=2(x1-1)2-4,
∴y=(x1-2)2-4,在[$\frac{7}{2}$,4)为增函数,
∴y∈[$\frac{21}{2}$,16)
故答案为:[$\frac{21}{2}$,16)
点评 本题考查分段函数,考查二次函数的性质,正确转化是解题的关键所在,属于中档题.

练习册系列答案
相关题目
19.若不等式x2-2x+a>0恒成立,则a的取值范围是( )
| A. | a<0 | B. | a<1 | C. | a>0 | D. | a>1 |
20.下列函数中哪个与函数y=x相等( )
| A. | y=($\sqrt{x}$)2 | B. | f(x)=$\frac{{x}^{2}}{x}$ | C. | y=|x| | D. | y=$\root{3}{{x}^{3}}$ |
18.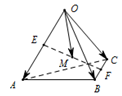 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |