题目内容

6．若数列{an}满足：对任意正整数n，{an+1-an}为递减数列，则称数列{an}为“差递减数列”．给出下列数列{an}（n∈N*）：
①an=3n，②an=n2+1，③an=$\sqrt{n}$，④an=2n-n，⑤an=ln$\frac{n}{n+1}$
其中是“差递减数列”的有（　　）
A．③⑤B．①②④C．③④⑤D．②③

分析 利用“差递减数列”的定义，通过作差an+1-an为递减数列即可判断得出．

解答 解：①∵an+1-an=3（n+1）-3n=3，∴数列{an}不为“差递减数列”．
同理可得：②④不为“差递减数列”．
③∵an+1-an=$\sqrt{n+1}-\sqrt{n}$=$\frac{1}{\sqrt{n+1}+\sqrt{n}}$，∴数列{an}为“差递减数列”．
同理可得：⑤为“差递减数列”．
故选：A．

点评 本题考查了“差递减数列”的定义、作差法、数列的单调性，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
16．已知一次函数f（x）在R上单调递增，当x∈[0，3]时，值域为[1，4]．
（1）求函数f（x）的解析式；
（2）当x∈[-1，8]时，求函数$g（x）=2x-\sqrt{f（x）}$的值域．
17．在△ABC中，内角A，B，C所对边的边长分别为a，b，c，已知2sin2$\frac{A}{2}$=$\sqrt{3}$sinA．
（I）求角A的大小；
（II）若$\frac{a}{c}$=2cosB，求$\frac{a}{b}$的值．
14．函数f（x）=|${log_{\frac{1}{2}}}$x|的单调递增区间是（　　）
A．$（0，\frac{1}{2}]$B．（1，2]C．[1，+∞）D．（0，+∞）
1．有下列四个命题，其中假命题是（　　）
A．?x0＞0，x02≤x0B．?x∈R，3x＞0
C．?x0∈R，sinx0+cosx0=2D．?x0∈R，lgx0=0
11．已知抛物线C：y2=4x，过焦点且与坐标轴不平行的直线与该抛物线相交于A、B两点，记线段AB中点为P（x0，y0）．
（Ⅰ）若x0=2，求直线AB的斜率；
（Ⅱ）设线段AB的垂直平分线与x轴，y轴分别相交于点D、E．当直线AB的斜率大于$\frac{{\sqrt{3}}}{3}$时，求$\frac{|AB|}{|DE|}$的取值范围．
18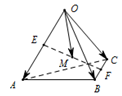．如图，E，F分别是四面体OABC的边OA，BC的中点，M为EF的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{OM}$相等的向量是（　　）
A．-$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$B．$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$C．$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$D．-$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$
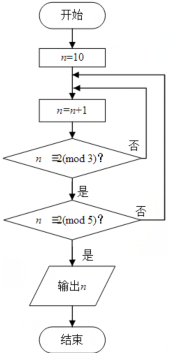15．已知双曲线C的右焦点为F，过F的直线l与双曲线C交于不同两点A、B，且A、B两点间的距离恰好等于焦距，若这样的直线l有且仅有两条，则双曲线C的离心率的取值范围为（1，$\frac{1+\sqrt{17}}{4}$）∪（2，+∞）．
16．若正整数N除以正整数m后的余数为n，则记为N=n（ mod m），例如10=2（mod 4）．如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》．执行该程序框图，则输出的n等于（　　）
A．20B．21C．22D．23

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网