题目内容
7.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,∠B=45°,△ABC的面积S=2(1)求边b的长;
(2)求△ABC的外接圆的面积.
分析 (1)先根据三角形面积公式求得c边的长,进而利用余弦定理求得b的值.
(2)根据正弦定理利用$\frac{b}{sinB}$=2R求得三角形外接圆的直径,根据圆的面积公式即可得解.
解答 解:(1)∵S=$\frac{1}{2}$acsinB=2,
∴$\frac{1}{2}$×1×c×sin45°=2,
∴c=4$\sqrt{2}$,
∴b2=a2+c2-2accosB=1+32-2×1×4$\sqrt{2}$×cos45°,
∴b2=25,b=5.
(2)∵b=5,∠B=45°,
∴△ABC的外接圆的直径等于$\frac{b}{sinB}$=5$\sqrt{2}$,可求△ABC的外接圆的面积S=π×($\frac{5\sqrt{2}}{2}$)2=$\frac{25π}{2}$.
点评 本题主要考查了三角形的面积公式,圆的面积公式,正弦定理和余弦定理在解三角形中的应用.作为正弦定理和余弦定理的变形公式也应熟练掌握,以便做题时方便使用,属于基础题.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
18.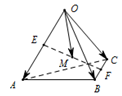 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
16.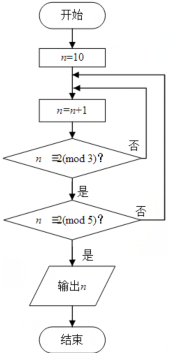 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
17.三位男同学两位女同学站成一排,女同学不站两端的排法总数为( )
| A. | 6 | B. | 36 | C. | 48 | D. | 120 |