题目内容
10．已知抛物线x2=-2y的一条弦AB的中点坐标为（-1，-5），则这条弦AB所在的直线方程是（ ）| A． | y=x-4 | B． | y=2x-3 | C． | y=-x-6 | D． | y=3x-2 |
分析 设A、B两点的坐标分别为（x1，y1），（x2，y2）则由E为AB的中点可得x1+x2=-2，x12=-2y1，x22=-2y2，两式相减可求直线AB的斜率，即可求出弦AB所在的直线方程．
解答 解：设A、B两点的坐标分别为（x1，y1），（x2，y2），则x1+x2=-2，x12=-2y1，x22=-2y2．
两式相减可得，（x1+x2）（x1-x2）=-2（y1-y2）
∴直线AB的斜率k=1，
∴弦AB所在的直线方程是y+5=x+1，即y=x-4．
故选A，
点评 此题主要强化了直线与圆锥曲线综合问题的考察．解题的关键是要根据中点坐标及直线AB的斜率．
练习册系列答案
期末集结号系列答案
相关题目
20．下列函数中哪个与函数y=x相等（ ）
| A． | y=（$\sqrt{x}$）2 | B． | f（x）=$\frac{{x}^{2}}{x}$ | C． | y=|x| | D． | y=$\root{3}{{x}^{3}}$ |
1．有下列四个命题，其中假命题是（ ）
| A． | ?x0＞0，x02≤x0 | B． | ?x∈R，3x＞0 | ||
| C． | ?x0∈R，sinx0+cosx0=2 | D． | ?x0∈R，lgx0=0 |
18．
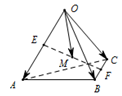如图，E，F分别是四面体OABC的边OA，BC的中点，M为EF的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{OM}$相等的向量是（ ）
如图，E，F分别是四面体OABC的边OA，BC的中点，M为EF的中点，若$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，则下列向量中与$\overrightarrow{OM}$相等的向量是（ ）| A． | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B． | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C． | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D． | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
5．一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了4次试验．收集的数据如下：
（Ⅰ）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；
（Ⅱ）现需生产20件此零件，预测需用多长时间？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$x）
| 零件个数x（个） | 1 | 2 | 3 | 4 |
| 加工时间y（小时） | 2 | 3 | 5 | 8 |
（Ⅱ）现需生产20件此零件，预测需用多长时间？
（参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$x）