题目内容
8.设函数f(x)=ex(3x-1)-ax+a,其中a<1,若有且只有一个整数x0使得f(x0)≤0,则a的取值范围是( )| A. | $(\frac{2}{e},\frac{3}{4})$ | B. | $[\frac{2}{e},\frac{3}{4})$ | C. | $(\frac{2}{e},1)$ | D. | $[\frac{2}{e},1)$ |
分析 设g(x)=ex(3x-1),h(x)=ax-a,对g(x)求导,将问题转化为存在唯一的整数x0使得g(x0)在直线h(x)=ax-a的下方,求导数可得函数的极值,解g(-1)-h(-1)=-4e-1+2a≥0,求得a的取值范围.
解答 解:设g(x)=ex(3x-1),h(x)=ax-a,
则g′(x)=ex(3x+2),
∴x∈(-∞,-$\frac{2}{3}$),g′(x)<0,g(x)单调递减,
x∈(-$\frac{2}{3}$,+∞),g′(x)>0,g(x)单调递增,
∴x=-$\frac{2}{3}$,取最小值-3e-$\frac{2}{3}$,
∴g(0)=-1<-a=h(0),
g(1)-h(1)=2e>0,
直线h(x)=ax-a恒过定点(1,0)且斜率为a,
∴g(-1)-h(-1)=-4e-1+2a>0,
∴a>$\frac{2}{e}$,
a<1,
∴a的取值范围($\frac{2}{e}$,1).
故选:C.
点评 本题考查求函数的导数,利用导数判断函数的单调性和极值问题,涉及转化的思想,属于中档题.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
18.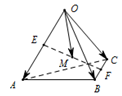 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
 如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )
如图,E,F分别是四面体OABC的边OA,BC的中点,M为EF的中点,若$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{OM}$相等的向量是( )| A. | -$\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | B. | $\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | C. | $\frac{1}{4}$$\overrightarrow{a}$-$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ | D. | -$\frac{1}{4}$$\overrightarrow{a}$+$\frac{1}{4}$$\overrightarrow{b}$+$\frac{1}{4}$$\overrightarrow{c}$ |
16.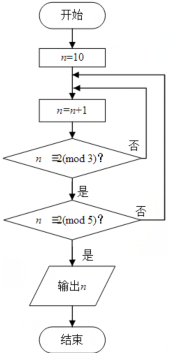 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
 若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )
若正整数N除以正整数m后的余数为n,则记为N=n( mod m),例如10=2(mod 4).如图程序框图的算法源于我国古代闻名中外的《中国剩余定理》.执行该程序框图,则输出的n等于( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
17.三位男同学两位女同学站成一排,女同学不站两端的排法总数为( )
| A. | 6 | B. | 36 | C. | 48 | D. | 120 |
 如图,在三棱锥S-ABC中,△ABC为直角三角形,且∠ACB=90°,SA⊥平面ABC,AD⊥SC.
如图,在三棱锥S-ABC中,△ABC为直角三角形,且∠ACB=90°,SA⊥平面ABC,AD⊥SC.