题目内容
函数f(x)=x4+(2-λ)x2+2-λ,是否存在实数λ,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数?若存在,请求出λ的值,若不存在,请说明理由.
考点:函数单调性的判断与证明
专题:导数的综合应用
分析:求f′(x),根据f′(x)的符号判断函数f(x)的单调性,求出函数f(x)在(-∞,0)上的单调赠区间:(-
,0)和单调减区间:(-∞,-
].所以要使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数,则能得到限制λ的不等式,解不等式,即得λ的取值,根据λ的取值,即能看出是否存在λ,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数.
|
|
解答:
解:f′(x)=4x3+2(2-λ)x=2x(2x2+2-λ);
若2-λ≥0,则函数f(x)在[-1,0)上是减函数,即不能使f(x)在[-1,0)上是增函数;
若2-λ<0,则令f′(x)=0得x=0,或±
;
∴x<-
时,2x<0,2x2+2-λ>0,∴f′(x)<0;-
<x<0时,2x<0,2x2+2-λ<0,∴f′(x)>0;
∴f(x)在(-∞,-
]上是减函数,在(-
,0)上是增函数;
∴若存在实数λ,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数,则:
,解得4≤λ≤6,不妨取λ=5;
即存在λ=5,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数.
若2-λ≥0,则函数f(x)在[-1,0)上是减函数,即不能使f(x)在[-1,0)上是增函数;
若2-λ<0,则令f′(x)=0得x=0,或±
|
∴x<-
|
|
∴f(x)在(-∞,-
|
|
∴若存在实数λ,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数,则:
|
即存在λ=5,使f(x)在(-∞,-2]上是减函数,而在[-1,0)上是增函数.
点评:考查通过求函数导数,根据导数符号判断函数单调性的方法,不要忘了讨论2-λ≥0和2-λ<0,求λ范围时可借助数轴.

练习册系列答案
相关题目
某几何体的三视图如图所示,则该几何体的外接球的球面面积为( )
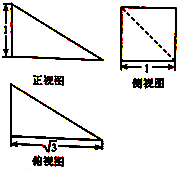

| A、5π | B、12π |
| C、20π | D、8π |
 如图,ABCD-A1B1C1D1为正方体,求证:平面A1C1CA⊥平面B1D1DB.
如图,ABCD-A1B1C1D1为正方体,求证:平面A1C1CA⊥平面B1D1DB.