题目内容
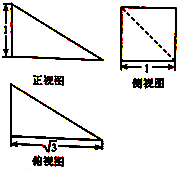
某几何体的三视图如图所示，则该几何体的外接球的球面面积为（ ）
| A、5π | B、12π |
| C、20π | D、8π |
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：三视图复原的几何体是底面为长、宽分别为3，4的长方形，侧棱垂直于底面的四棱锥；把它扩展为长方体，它的外接球的直径就是长方体的对角线的长，求出对角线长，即可求出外接球的表面积．
解答：
解：三视图复原的几何体是底面为长、宽分别为3，4的长方形，侧棱垂直于底面的四棱锥；把它扩展为长方体，
则长、宽、高分别为1，1，
，
则它的外接球的直径就是长方体的对角线的长，
所以长方体的对角线长为：
=
所以球的半径为：R=
．
这个几何体的外接球的表面积是：4πR2=5π．
故选：A
则长、宽、高分别为1，1，
| 3 |
则它的外接球的直径就是长方体的对角线的长，
所以长方体的对角线长为：
| 1+1+3 |
| 5 |
所以球的半径为：R=
| ||
| 2 |
这个几何体的外接球的表面积是：4πR2=5π．
故选：A
点评：本题是基础题，考查几何体的外接球的问题，空间想象能力，逻辑思维能力，和计算能力，注意本题中三棱锥的外接球与长方体的外接球是同一个球．
练习册系列答案
相关题目
已知函数f（x）=log
cos
，x∈（0，1），函数g（x）=asin（
x）-2a+2（a＞0），x∈（0，1）．若存在x1，x2∈（0，1），使得f（x1）=g（x2）成立，则实数a的取值范围是（ ）
| 1 |
| 2 |
| πx |
| 3 |
| π |
| 6 |
A、（
| ||||
B、（
| ||||
C、（
| ||||
D、（
|
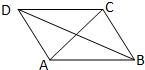如图平行四边形ABCD中，| AC |
| BD |
| AD |
| AC |
| A、1 | B、2 | C、3 | D、4 |
函数y=
的定义域为（ ）
| ||
| x-2 |
| A、{x|x≠2} |
| B、{x|x≥0且x≠2} |
| C、{x|x≥0} |
| D、{x|x≥1且x≠2} |
方程lnx+2x-8=0的实数根的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
两个平面能把空间分成几个部分（ ）
| A、2或3 | B、3或4 |
| C、3 | D、2或4 |
某中学有学生270人（其中一年级108人，二、三年级各81人），将学生按一、二、三年级依次统一编号为1，2，…，270，现考虑选用简单随机抽样、分层抽样和系统抽样三种方案从中抽取10人参加某项调查，如果抽得号码有下列四种情况：
①7，34，61，88，115，142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（ ）
①7，34，61，88，115，142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（ ）
| A、②、③都不能为系统抽样 |
| B、②、④都不能为分层抽样 |
| C、③、④都可能为系统抽样 |
| D、①、③都可能为分层抽样 |
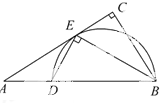如图，在Rt△ABC中，∠=90°，BE平分∠ABC，交AC于点E，点D在AB上，DE⊥EB．