题目内容
二次函数f(x)满足f(x+1)-f(x)=2x+3,且f(0)=-3.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设圆C经过上述二次函数的图象与两坐标轴的三个交点,求圆C的方程;
(Ⅲ)设直线l1:mx-y+2=0与(Ⅱ)中的圆C交于A,B两点,是否存在实数m,使得过点P(1,1)的直线l2垂直平分弦AB?若存在,求出实数m的值;若不存在,请说明理由.
(Ⅰ)求f(x)的解析式;
(Ⅱ)设圆C经过上述二次函数的图象与两坐标轴的三个交点,求圆C的方程;
(Ⅲ)设直线l1:mx-y+2=0与(Ⅱ)中的圆C交于A,B两点,是否存在实数m,使得过点P(1,1)的直线l2垂直平分弦AB?若存在,求出实数m的值;若不存在,请说明理由.
考点:圆的标准方程,直线与圆的位置关系
专题:直线与圆
分析:(Ⅰ)设f(x)=ax2+bx+c,(a≠0),则由f(0)=-3,得c=-3,由此能求出f(x)=x2+2x-3.
(Ⅱ)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,令y=0,得x2+Dx+F=0,从而D=2,F=-3,令x=0,得y2+Ey+F=0,此方程有一个根为-3,代入得出E=2,由此能求出圆C的方程.
(Ⅲ)把直线mx-y+2=0,即y=mx+2,代入圆C的方程,得(m2+1)x2+(6m+2)x+5=0,由于直线mx-y+2=0交圆C于A,B两点,由△>0得m<-2或m>
,设符合条件的实数m存在,解得m=-1不满足△>0,从而不存在实数m,使得过点P(2,0)的直线l2垂直平分弦AB.
(Ⅱ)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,令y=0,得x2+Dx+F=0,从而D=2,F=-3,令x=0,得y2+Ey+F=0,此方程有一个根为-3,代入得出E=2,由此能求出圆C的方程.
(Ⅲ)把直线mx-y+2=0,即y=mx+2,代入圆C的方程,得(m2+1)x2+(6m+2)x+5=0,由于直线mx-y+2=0交圆C于A,B两点,由△>0得m<-2或m>
| 1 |
| 2 |
解答:
解:(Ⅰ)设f(x)=ax2+bx+c,(a≠0),
则由f(0)=-3,得c=-3,
f(x+1)-f(x)=a(x+1)2+b(x+1)-(ax2+bx)=2ax+a+b=2x+3,
∴
,解得a=1,b=2,
∴f(x)=x2+2x-3.
(Ⅱ)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,
令y=0,得x2+Dx+F=0,
这与x2+2x-3=0是同一个方程,
∴D=2,F=-3,
令x=0,得y2+Ey+F=0,此方程有一个根为-3,代入得出E=2,
∴圆C的方程为x2+y2+2x+2y-3=0,
即(x+1)2+(y+1)2=5.
(Ⅲ)把直线mx-y+2=0,即y=mx+2,代入圆C的方程,
消去y,整理得(m2+1)x2+(6m+2)x+5=0,
由于直线mx-y+2=0交圆C于A,B两点,
故△=4(3m+1)2-20(m2+1)>0,
即2m2+3m-2>0,解得m<-2或m>
,(*)
设符合条件的实数m存在,
由于l2垂直平分弦AB,故圆心C(-1,-1)必在l2上,
∴l2的斜率kPC=1,而kAB=m=-
,
∴m=-1不满足(*)式,
故不存在实数m,使得过点P(2,0)的直线l2垂直平分弦AB.
则由f(0)=-3,得c=-3,
f(x+1)-f(x)=a(x+1)2+b(x+1)-(ax2+bx)=2ax+a+b=2x+3,
∴
|
∴f(x)=x2+2x-3.
(Ⅱ)设所求圆的一般方程为x2+y2+Dx+Ey+F=0,
令y=0,得x2+Dx+F=0,
这与x2+2x-3=0是同一个方程,
∴D=2,F=-3,
令x=0,得y2+Ey+F=0,此方程有一个根为-3,代入得出E=2,
∴圆C的方程为x2+y2+2x+2y-3=0,
即(x+1)2+(y+1)2=5.
(Ⅲ)把直线mx-y+2=0,即y=mx+2,代入圆C的方程,
消去y,整理得(m2+1)x2+(6m+2)x+5=0,
由于直线mx-y+2=0交圆C于A,B两点,
故△=4(3m+1)2-20(m2+1)>0,
即2m2+3m-2>0,解得m<-2或m>
| 1 |
| 2 |
设符合条件的实数m存在,
由于l2垂直平分弦AB,故圆心C(-1,-1)必在l2上,
∴l2的斜率kPC=1,而kAB=m=-
| 1 |
| kPC |
∴m=-1不满足(*)式,
故不存在实数m,使得过点P(2,0)的直线l2垂直平分弦AB.
点评:本题考查函数解析式的求法,考查圆的方程的求法,考查满足条件的实数是否存在的判断与求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
函数y=
的定义域为( )
| ||
| x-2 |
| A、{x|x≠2} |
| B、{x|x≥0且x≠2} |
| C、{x|x≥0} |
| D、{x|x≥1且x≠2} |
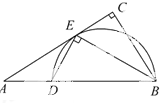 如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.
如图,在Rt△ABC中,∠=90°,BE平分∠ABC,交AC于点E,点D在AB上,DE⊥EB.