题目内容
乒乓球赛规定：一局比赛，双方比分在10平前，一方连续发球2次后，对方再连续发球2次，依次轮换，每次发球，胜方得1分，负方得0分．设在甲、乙的比赛中，每次发球，发球方得1分的概率为
，各次发球的胜负结果相互独立，甲、乙的一局比赛中，甲先发球．
（Ⅰ）求开始第4次发球时，甲、乙的比分为1比2的概率；
（Ⅱ）ξ表示开始第4次发球时乙的得分，求ξ的分布列与数学期望．
| 3 |
| 5 |
（Ⅰ）求开始第4次发球时，甲、乙的比分为1比2的概率；
（Ⅱ）ξ表示开始第4次发球时乙的得分，求ξ的分布列与数学期望．
考点：离散型随机变量及其分布列,离散型随机变量的期望与方差
专题：概率与统计
分析：（1）记Ai为事件“第i次发球，甲胜”，i=1，2，3，则P（A1）=P（A2）=
，P（A3）=
．“开始第4次发球时，甲、乙的比分为1比2”为事件A1
+
A2
+
A3，由此能求出开始第4次发球时，甲、乙的比分为1比2的概率．
（2）由题意ξ=0，1，2，3．分别求出P（ξ=0），P（ξ=1），P（ξ=2），P（ξ=3），由此能求出Eξ．
| 3 |
| 5 |
| 2 |
| 5 |
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
（2）由题意ξ=0，1，2，3．分别求出P（ξ=0），P（ξ=1），P（ξ=2），P（ξ=3），由此能求出Eξ．
解答：
解：（1）记Ai为事件“第i次发球，甲胜”，i=1，2，3，
则P（A1）=P（A2）=
，P（A3）=
．
“开始第4次发球时，甲、乙的比分为1比2”为事件
A1
+
A2
+
A3，
其概率为
P（A1
+
A2
+
A3）=2×
×
×
+
×
×
=
，
即开始第4次发球时，甲、乙的比分为1比2的概率为
．…（6分）
（2）由题意ξ=0，1，2，3．
P（ξ=0）=
×
×
=
，
P（ξ=1）=2×
×
×
+（
）3=
，
P（ξ=2）=2×
×
×
+
×
×
=
，
P（ξ=3）=
×
×
=
，
∴ξ的分布列为：
所以Eξ=0×
+1×
+2×
+3×
=
．…（12分）
则P（A1）=P（A2）=
| 3 |
| 5 |
| 2 |
| 5 |
“开始第4次发球时，甲、乙的比分为1比2”为事件
A1
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
其概率为
P（A1
. |
| A2 |
. |
| A3 |
. |
| A1 |
. |
| A3 |
. |
| A1 |
. |
| A2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 44 |
| 125 |
即开始第4次发球时，甲、乙的比分为1比2的概率为
| 44 |
| 125 |
（2）由题意ξ=0，1，2，3．
P（ξ=0）=
| 3 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 18 |
| 125 |
P（ξ=1）=2×
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 51 |
| 125 |
P（ξ=2）=2×
| 3 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 5 |
| 44 |
| 125 |
P（ξ=3）=
| 2 |
| 5 |
| 2 |
| 5 |
| 3 |
| 5 |
| 12 |
| 125 |
∴ξ的分布列为：
| ξ | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 18 |
| 125 |
| 51 |
| 125 |
| 44 |
| 125 |
| 12 |
| 125 |
| 7 |
| 5 |
点评：本题考查离散型随机变量的分布列和数学期望，是历年高考的必考题型．解题时要认真审题，仔细解答，注意概率知识的合理运用．
练习册系列答案
相关题目
两个平面能把空间分成几个部分（ ）
| A、2或3 | B、3或4 |
| C、3 | D、2或4 |
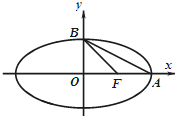如图，椭圆C：