题目内容
已知矩阵M=
（1）试求M的逆矩阵；
（2）求M的特征值及特征向量．
|
（1）试求M的逆矩阵；
（2）求M的特征值及特征向量．
考点：特征值与特征向量的计算
专题：计算题,矩阵和变换
分析：（1）设出逆矩阵，由定义得到方程，解出系数a，b，c，d即可．
（2）先根据特征值的定义列出特征多项式，令f（λ）=0解方程可得特征值，再由特征值列出方程组即可解得相应的特征向量．
（2）先根据特征值的定义列出特征多项式，令f（λ）=0解方程可得特征值，再由特征值列出方程组即可解得相应的特征向量．
解答：
解：（1）设M的逆矩阵为
，
则
•
=
，
则
，解得
，
故逆矩阵为
．
（2）由f（λ）=
=（λ-3）（λ-1）=0，
解得λ=3或λ=1，
设λ=3对应的一个特征向量为α=
则
，得y=0，x=0．
则当λ=3时，对应的特征向量为α1=
，
同理可得，当λ=1时，对应的特征向量为α2=
．
|
则
|
|
|
则
|
|
故逆矩阵为
|
（2）由f（λ）=
|
解得λ=3或λ=1，
设λ=3对应的一个特征向量为α=
|
则
|
则当λ=3时，对应的特征向量为α1=
|
同理可得，当λ=1时，对应的特征向量为α2=
|
点评：本题主要考查了矩阵特征值与特征向量以及逆矩阵的计算等基础知识，属于基础题．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
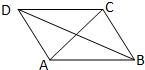如图平行四边形ABCD中，| AC |
| BD |
| AD |
| AC |
| A、1 | B、2 | C、3 | D、4 |
某中学有学生270人（其中一年级108人，二、三年级各81人），将学生按一、二、三年级依次统一编号为1，2，…，270，现考虑选用简单随机抽样、分层抽样和系统抽样三种方案从中抽取10人参加某项调查，如果抽得号码有下列四种情况：
①7，34，61，88，115，142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（ ）
①7，34，61，88，115，142，169，196，223，250；
②5，9，100，107，111，121，180，195，200，265；
③11，38，65，92，119，146，173，200，227，254；
④30，57，84，111，138，165，192，219，246，270；
关于上述样本的下列结论中，正确的是（ ）
| A、②、③都不能为系统抽样 |
| B、②、④都不能为分层抽样 |
| C、③、④都可能为系统抽样 |
| D、①、③都可能为分层抽样 |
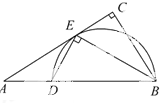如图，在Rt△ABC中，∠=90°，BE平分∠ABC，交AC于点E，点D在AB上，DE⊥EB．