题目内容
函数f(x)=
的值域为 .
| x+1 |
| x2+1 |
考点:函数的值域
专题:函数的性质及应用
分析:本题通过换元法,将分子换成t,然后分类讨论,求出分母的取值范围,得到f(x)=
的值域,即得到本题结论.
| x+1 |
| x2+1 |
解答:
解:设x+1=t,则x=t-1,
∵函数f(x)=
,
∴记g(t)=
=
,
(1)当t=0时,g(t)=0,
(2)当t≠0时,g(t)=
,
∵t+
≤-2
或t+
≥2
,
∴t+
-2≤-2
-2或t+
-2≥2
-2,
∴
≤
<0或0<
≤
,
∴
≤g(t)<0或0<g(t)≤
,
综上,
≤g(t)≤
,
∴函数f(x)=
的值域为{y|
≤y≤
},
故答案为:[
,
].
∵函数f(x)=
| x+1 |
| x2+1 |
∴记g(t)=
| t |
| (t-1)2+1 |
| t |
| t2-2t+2 |
(1)当t=0时,g(t)=0,
(2)当t≠0时,g(t)=
| 1 | ||
t+
|
∵t+
| 2 |
| t |
| 2 |
| 2 |
| t |
| 2 |
∴t+
| 2 |
| t |
| 2 |
| 2 |
| t |
| 2 |
∴
| 1 | ||
-2
|
| 1 | ||
t+
|
| 1 | ||
t+
|
| 1 | ||
2
|
∴
1-
| ||
| 2 |
1+
| ||
| 2 |
综上,
1-
| ||
| 2 |
1+
| ||
| 2 |
∴函数f(x)=
| x+1 |
| x2+1 |
1-
| ||
| 2 |
1+
| ||
| 2 |
故答案为:[
1-
| ||
| 2 |
1+
| ||
| 2 |
点评:本题考查了换元法求二次分式函数的值域,本题也可利用导函数研究,本题难度不大,属于基础题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
集合A={x|-7<x<3},集合B={x|1<x<7},则A∪B=( )
| A、{x|-7<x<7} |
| B、{x|1<x<7} |
| C、{x|-7<x<3} |
| D、{x|1<x<3} |
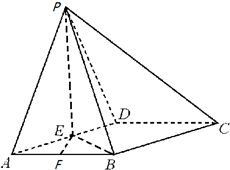 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为正三角形,且E,F分别为AD,AB的中点,PE⊥平面ABCD,BE⊥平面PAD.