题目内容
10.设奇函数f(x)在(0,+∞)上为减函数,且f(1)=0,则不等式$\frac{2f(x)-f(x)}{3x}$<0的解集为( )| A. | (-1,0)∪(1,+∞) | B. | (-∞,-1)∪(0,1) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,0)∪(0,1) |
分析 本题可以利用f(x)在(0,+∞)上为减函数,且f(1)=0,得到f(x)的相应函数值的正负情况,再根据f(x)是奇函数,得到在(-∞,0)上f(x)的相应函数值的正负情况,通过分类讨论,将不等式$\frac{2f(x)-f(x)}{3x}$<0等价于不等式xf(x)<0,转化为不等式组,解不等式组,得到本题结论.
解答 解:∵f(x)在(0,+∞)上为减函数,且f(1)=0,
∴当0<x<1时,f(x)>0;
当x>1时,f(x)<0.
又∵f(x)是奇函数,
∴由图象的对称性知:当x<-1时,f(x)>0;
当-1<x<0时,f(x)<0.
若f(0)有意义,则f(0)=0.
∵不等式$\frac{2f(x)-f(x)}{3x}$<0等价于不等式xf(x)<0,
∴$\left\{\begin{array}{l}{x>0}\\{f(x)<0}\end{array}\right.$或$\left\{\begin{array}{l}{x<0}\\{f(x)>0}\end{array}\right.$,
∴x>1或x<-1.
故选:C.
点评 本题考查了函数的单调性与对称性,函数性质与图象间关系,本题难度不大,属于基础题.

练习册系列答案
相关题目
20.某城市现有人口总数为1000万人,如果年自然增长率为0.9%,试解答下面的问题:
(1)写出该城市人口总数y与年份x的函数关系式;
(2)计算大约多少年后该城市人口将达到1100万人(精确到1年).
(1)写出该城市人口总数y与年份x的函数关系式;
(2)计算大约多少年后该城市人口将达到1100万人(精确到1年).
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-3y+4≥0,}&{\;}\\{x+2y-1≥0,}&{\;}\\{3x+y-8≤0.}&{\;}\end{array}\right.$,则z=2x-y的最小值与最大值分别为( )
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
5.已知数列{an}的首项a1=1,其前n项和Sn=$\frac{(n+1){a}_{n}}{2}$.则(1-$\frac{1}{{S}_{2}}$)(1-$\frac{1}{{S}_{3}}$)(1-$\frac{1}{{S}_{4}}$)…(1-$\frac{1}{{S}_{2016}}$)的值为( )
| A. | $\frac{2015}{3024}$ | B. | $\frac{2015}{4032}$ | C. | $\frac{1009}{2016}$ | D. | $\frac{1009}{3024}$ |
19.过原点且倾斜角为30°的直线l被圆C:x2+y2+4y-3=0所截得的弦长为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | 2$\sqrt{3}$ | D. | 4 |
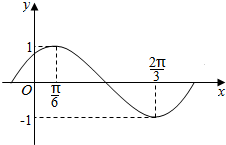 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.