题目内容
12.向量$\overrightarrow{a}$、$\overrightarrow{b}$之间的夹角为30°,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,求$\overrightarrow{a}$•$\overrightarrow{b}$,$\overrightarrow{a}$2,$\overrightarrow{b}$2,($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$).分析 利用数量积公式可得$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos30°,$\overrightarrow{a}$2=|$\overrightarrow{a}$|2,$\overrightarrow{b}$2=|$\overrightarrow{b}$|2,($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)=|$\overrightarrow{a}$|2+$\overrightarrow{a}$•$\overrightarrow{b}$-2|$\overrightarrow{b}$|2.
解答 解:∵向量$\overrightarrow{a}$、$\overrightarrow{b}$之间的夹角为30°,且|$\overrightarrow{a}$|=3,|$\overrightarrow{b}$|=4,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|•cos30°=3×4×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
$\overrightarrow{a}$2=|$\overrightarrow{a}$|2=9,
$\overrightarrow{b}$2=|$\overrightarrow{b}$|2=16,
($\overrightarrow{a}$+2$\overrightarrow{b}$)•($\overrightarrow{a}$-$\overrightarrow{b}$)
=|$\overrightarrow{a}$|2+$\overrightarrow{a}$•$\overrightarrow{b}$-2|$\overrightarrow{b}$|2
=9+6$\sqrt{3}$-32
=6$\sqrt{3}$-23.
点评 本题考查向量数量积定义的应用.

 习题精选系列答案
习题精选系列答案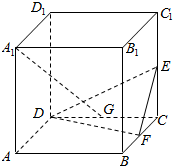 如图,正方体ABCD-A1B1C1D1中,E,F,G分别是棱CC1,BC,CD的中点,求证:A1G⊥平面DEF.
如图,正方体ABCD-A1B1C1D1中,E,F,G分别是棱CC1,BC,CD的中点,求证:A1G⊥平面DEF.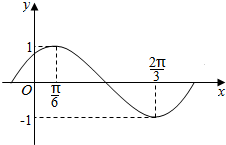 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.