题目内容
13.已知直线x+4y=2与x轴,y轴分别交于A,B两点,若动点P(a,b)在线段AB上,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )| A. | $\frac{7}{2}$ | B. | 4 | C. | $\frac{9}{2}$ | D. | 5 |
分析 由题意a+4b=2,且a>0,b>0,所以$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{2}$(a+4b)($\frac{1}{a}$+$\frac{1}{b}$)=$\frac{1}{2}$(5+$\frac{4b}{a}$+$\frac{a}{b}$)≥$\frac{1}{2}$(5+4)=$\frac{9}{2}$,可求得$\frac{1}{a}$+$\frac{1}{b}$的最小值.
解答 解:由题意知a+4b=2,且a>0,b>0,
所以$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{2}$(a+4b)($\frac{1}{a}$+$\frac{1}{b}$)=$\frac{1}{2}$(5+$\frac{4b}{a}$+$\frac{a}{b}$)≥$\frac{1}{2}$(5+4)=$\frac{9}{2}$,
当且仅当$\frac{4b}{a}$=$\frac{a}{b}$,即a=$\frac{2}{3}$,b=$\frac{1}{3}$时,取等号,即$\frac{1}{a}$+$\frac{1}{b}$的最小值为$\frac{9}{2}$.
故选:C.
点评 本题主要考查求$\frac{1}{a}$+$\frac{1}{b}$的最小值,考查基本不等式的运用,正确运用基本不等式是关键.

练习册系列答案
相关题目
18.设x,y满足约束条件$\left\{\begin{array}{l}{x-3y+4≥0,}&{\;}\\{x+2y-1≥0,}&{\;}\\{3x+y-8≤0.}&{\;}\end{array}\right.$,则z=2x-y的最小值与最大值分别为( )
| A. | -3与7 | B. | 2与3 | C. | 2与7 | D. | 3与7 |
5.已知数列{an}的首项a1=1,其前n项和Sn=$\frac{(n+1){a}_{n}}{2}$.则(1-$\frac{1}{{S}_{2}}$)(1-$\frac{1}{{S}_{3}}$)(1-$\frac{1}{{S}_{4}}$)…(1-$\frac{1}{{S}_{2016}}$)的值为( )
| A. | $\frac{2015}{3024}$ | B. | $\frac{2015}{4032}$ | C. | $\frac{1009}{2016}$ | D. | $\frac{1009}{3024}$ |
3.已知点A(3,6),B(1,4),C(1,0),则△ABC的外接圆的圆心坐标为( )
| A. | (5,2) | B. | (-5,2) | C. | (2,5) | D. | (5,-2) |
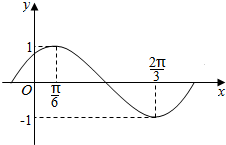 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.