题目内容
如图为一个几何体的三视图,求这个几何体的表面积和体积.


考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:判断几何体的形状,然后利用三视图的数据求解几何体的表面积与体积.
解答:
解:几何体是圆柱挖去一个同底等高的倒放的圆锥,圆柱的底面半径为1,高为3,
∴S表=S圆柱侧+S圆锥侧+S底=2π×1×3+
×2π×1×
+π×12=7π+
π(cm2),
V=V圆柱-V圆锥=
V圆柱=
×π×12×3=2π(cm3).
∴S表=S圆柱侧+S圆锥侧+S底=2π×1×3+
| 1 |
| 2 |
| 12+32 |
| 10 |
V=V圆柱-V圆锥=
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查三视图与几何体的关系,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
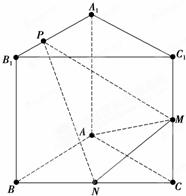 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且