题目内容
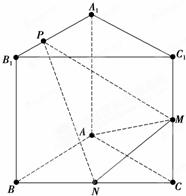 如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且
如图,已知三棱柱ABC-A1B1C1的侧棱与底面垂直,AA1=AB=AC=1,AB⊥AC,M、N分别是CC1,BC的中点,点P在线段A1B1上,且| A1P |
| A1B1 |
(1)证明:无论λ取何值,总有AM⊥PN;
(2)当λ=
| 1 |
| 2 |
考点:直线与平面所成的角,直线与平面垂直的性质
专题:综合题,空间位置关系与距离,空间角
分析:(1)以A为坐标原点,分别以AB,AC,AA1为x,y,z轴,建立空间直角坐标系,利用向量法能证明无论λ取何值,总有AM⊥PN.
(2)求出
和平面ABC的法向量,利用向量法能求出直线PN与平面ABC所成角的正切值.
(2)求出
| PN |
解答:
 (1)证明:以A为坐标原点,分别以AB,AC,AA1为x,y,z轴,建立空间直角坐标系,
(1)证明:以A为坐标原点,分别以AB,AC,AA1为x,y,z轴,建立空间直角坐标系,
由题意知:A1(0,0,1),B1(1,0,1),M(0,1,
),N(
,
,0),
∴
=λ
=(λ,0,0),
=(λ,0,1),
=(
-λ,
,-1),
∵
=(0,1,
),∴
•
=0,
∴无论λ取何值,总有AM⊥PN.…(6分)
(2)解:λ=
时,
=(0,
,-1),
由题意知平面ABC的法向量
=(0,0,1)…(8分)
设α为PN与面ABC所成角,
则sinα=|cos<
,
>|=
,…(12分)
∴tanα=2,
∴直线PN与平面ABC所成角的正切值为2.…(13分)
 (1)证明:以A为坐标原点,分别以AB,AC,AA1为x,y,z轴,建立空间直角坐标系,
(1)证明:以A为坐标原点,分别以AB,AC,AA1为x,y,z轴,建立空间直角坐标系,由题意知:A1(0,0,1),B1(1,0,1),M(0,1,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
| A1P |
| A1B1 |
| AP |
| PN |
| 1 |
| 2 |
| 1 |
| 2 |
∵
| AM |
| 1 |
| 2 |
| AM |
| PN |
∴无论λ取何值,总有AM⊥PN.…(6分)
(2)解:λ=
| 1 |
| 2 |
| PN |
| 1 |
| 2 |
由题意知平面ABC的法向量
| n |
设α为PN与面ABC所成角,
则sinα=|cos<
| PN |
| n |
2
| ||
| 5 |
∴tanα=2,
∴直线PN与平面ABC所成角的正切值为2.…(13分)
点评:本题考查的知识点是异面直线垂直的证明,考查直线与平面所成角的正切值的求法,其中熟练掌握向量夹角公式是解答此类问题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
“a=1”是“复数a2-1+(a+1)i(a∈R,i为虚数单位)是纯虚数”的( )
| A、充分不必要 |
| B、必要不充分 |
| C、充要条件 |
| D、既不充分也不必要 |