题目内容
已知方程ax2+bx+2=0的两根为-
和2.
(1)求a、b的值;
(2)解不等式ax2+bx-1>0.
| 1 |
| 2 |
(1)求a、b的值;
(2)解不等式ax2+bx-1>0.
考点:一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)利用根与系数的关系即可得出;
(2)利用一元二次不等式的解法即可得出.
(2)利用一元二次不等式的解法即可得出.
解答:
解:(1)∵方程ax2+bx+2=0的两根为-
和2,
由根与系数的关系,得
,
解得a=-2,b=3.
(2)由(1)知,不等式ax2+bx-1>0,
即为-2x2+3x-1>0,化为2x2-3x+1<0.解得
<x<1.
∴不等式ax2+bx-1>0的解集为{x|
<x<1}.
| 1 |
| 2 |
由根与系数的关系,得
|
解得a=-2,b=3.
(2)由(1)知,不等式ax2+bx-1>0,
即为-2x2+3x-1>0,化为2x2-3x+1<0.解得
| 1 |
| 2 |
∴不等式ax2+bx-1>0的解集为{x|
| 1 |
| 2 |
点评:本题考查了一元二次方程的根与系数的关系、一元二次不等式的解法,属于基础题.

练习册系列答案
相关题目
已知实数x,y满足方程x2+y2-4x+1=0,则
的取值范围是( )
| y |
| x+1 |
| A、[-1,1] | ||||||||
B、[-
| ||||||||
C、[-
| ||||||||
D、[0,
|
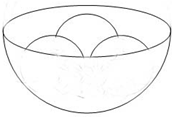 如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是
如图,三个半径都是10cm的小球放在一个半球面的碗中,小球的顶端恰好与碗的上沿处于同于水平面,则这个碗的半径R是