题目内容
已知等比数列{an}的前n项和为Sn，且S5=2，S10=6，则a16+a17+a18+a19+a20=（ ）
| A、54 | B、48 | C、32 | D、16 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：根据题意和等比数列的片段和性质得：S5、S10-S5、S15-S10、S20-S15…成首项是2、公比也是2等比数列，由等比数列的通项公式求出S20-S15的值，即可得答案．
解答：
解：由题意得S5=2，S10=6，S10-S5=4，
因为等比数列中S5、S10-S5、S15-S10、S20-S15…成等比数列，
所以此等比数列的首项是2、公比也是2，
则S20-S15=2×8=16，即a16+a17+a18+a19+a20=16，
故选：D．
因为等比数列中S5、S10-S5、S15-S10、S20-S15…成等比数列，
所以此等比数列的首项是2、公比也是2，
则S20-S15=2×8=16，即a16+a17+a18+a19+a20=16，
故选：D．
点评：本题考查等比数列的片段和性质，等比数列的通项公式的灵活应用，是常考的题．
练习册系列答案
相关题目
设Sn是等差数列{an}的前n项和，已知a5=9，S2=4，则a2=（ ）
| A、1 | B、2 | C、3 | D、5 |
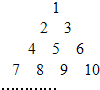如图，自然数列按正三角形图顺序排列，如数9排在第4行第3个位置；设数2015排在第m行第n个位置，则m+n=在△ABC中，
=（cos18°，sin18°），
=（2cos63°，2cos27°）则面积为（ ）
| AB |
| BC |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
