题目内容
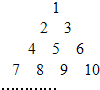 如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=
如图,自然数列按正三角形图顺序排列,如数9排在第4行第3个位置;设数2015排在第m行第n个位置,则m+n=考点:归纳推理
专题:推理和证明
分析:本题根据图形排列的规律,发现每一行的最后一个数是正整数数列的前n项和,从而可以求出第m-1行的最后一个数,从而算出m的值,然后推导出第m行的第n个数的表达式,从而求出n的值,得到m+n的值,得到本题结论.
解答:
解:∵如图,自然数列按正三角形图顺序排列,
∴第1行最后一个为:1,
第2行最后一个为:1+2=3,
第3行最后一个为:1+2+3,
第4行最后一个为:1+2+3+4,
…
第m-1行最后一个数为:1+2+3+…+(m-1)=
×(m-1)=
.
∵数2015排在第m行第n个位置,
∴
<2015≤
,m∈N*,
且2015=
+n,
∴m=63,n=62.
∴m+n=125.
故答案为:125.
∴第1行最后一个为:1,
第2行最后一个为:1+2=3,
第3行最后一个为:1+2+3,
第4行最后一个为:1+2+3+4,
…
第m-1行最后一个数为:1+2+3+…+(m-1)=
| 1+(m-1) |
| 2 |
| m(m-1) |
| 2 |
∵数2015排在第m行第n个位置,
∴
| m(m-1) |
| 2 |
| m(m+1) |
| 2 |
且2015=
| m(m-1) |
| 2 |
∴m=63,n=62.
∴m+n=125.
故答案为:125.
点评:本题考查了归纳推理、等差数列的求和,还考查了取整思想,本题难度不大,属于基础题.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
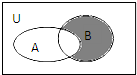 设集合U={1,2,3,4,5},A={2,3,4},B={3,5},则图中阴影部分所表示的集合为( )
设集合U={1,2,3,4,5},A={2,3,4},B={3,5},则图中阴影部分所表示的集合为( )| A、{2,3} | B、{1,4} |
| C、{5} | D、{6} |
已知等比数列{an}的前n项和为Sn,且S5=2,S10=6,则a16+a17+a18+a19+a20=( )
| A、54 | B、48 | C、32 | D、16 |
设A,B为抛物线y2=2px(p>0)上不同的两点,O为坐标原点,且OA⊥OB,则△OAB面积的最小值为( )
| A、p2 |
| B、2p2 |
| C、4p2 |
| D、6p2 |
