题目内容
设函数f(x)=ax2+bx+c(a,b,c∈R).若x=-1为函数f(x)ex的一个极值点,则如图四个图象可以为y=f(x)的图象序号是 (写出所有满足题目条件的序号).
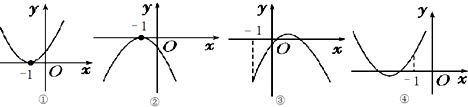
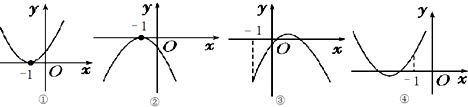
考点:利用导数研究函数的极值,二次函数的性质
专题:函数的性质及应用,导数的概念及应用
分析:先求出函数f(x)ex的导函数,利用x=-1为函数f(x)ex的一个极值点可得a,b,c之间的关系,再代入函数f(x)=ax2+bx+c,对答案分别代入验证,看哪个答案不成立即可.
解答:
解:因为[f(x)ex]′=f′(x)ex+f(x)(ex)′=[f(x)+f′(x)]ex,
且x=-1为函数f(x)ex的一个极值点,所以f(-1)+f′(-1)=0;
对于①②,f(-1)=0且f′(-1)=0,所以成立;
对于③,f(-1)<0,且a<0,-
<-1,得2a-b<0,即b-2a>0,
所以f′(-1)>0,
所以可满足f(-1)+f′(-1)=0,故③可以成立;
对于④,因f(-1)>0,f′(-1)>0,不满足f′(1)+f(1)=0,故不能成立,
故①②③成立.
故答案为:①②③
且x=-1为函数f(x)ex的一个极值点,所以f(-1)+f′(-1)=0;
对于①②,f(-1)=0且f′(-1)=0,所以成立;
对于③,f(-1)<0,且a<0,-
| b |
| 2a |
所以f′(-1)>0,
所以可满足f(-1)+f′(-1)=0,故③可以成立;
对于④,因f(-1)>0,f′(-1)>0,不满足f′(1)+f(1)=0,故不能成立,
故①②③成立.
故答案为:①②③
点评:本题考查极值点与导函数之间的关系.一般在知道一个函数的极值点时,直接把极值点代入导数令其等0即可.可导函数的极值点一定是导数为0的点,但导数为0的点不一定是极值点.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
已知等比数列{an}的前n项和为Sn,且S5=2,S10=6,则a16+a17+a18+a19+a20=( )
| A、54 | B、48 | C、32 | D、16 |
已知角A是△ABC的一个内角,若sinA+cosA=
,则tanA等于( )
| 7 |
| 13 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
等差数列中,如果a4+a6=22,则前9项的和为( )
| A、297 | B、144 |
| C、99 | D、66 |
下列函数中,与函数y=
定义域相同的函数为( )
| 1 | ||
|
A、y=
| ||
B、y=
| ||
| C、y=x-2 | ||
| D、y=lnx |