题目内容

已知函数f（x）=
log2x，x＞0
3x，x≤0
，则f（f（log3
1
2
））=
 
．
考点：函数的值
专题：函数的性质及应用
分析：利用分段函数的性质求解．
解答： 解：∵函数f（x）=
log2x，x＞0
3x，x≤0
，
∴f（log3
1
2
）=3log3
1
2
=
1
2
，
f（f（log3
1
2
））=f（
1
2
）=log2
1
2
=-1．
故答案为：-1．
点评：本题考查函数的性质的合理运用，是基础题，解题时要认真审题，注意分段函数的性质的合理运用．
练习册系列答案
相关题目
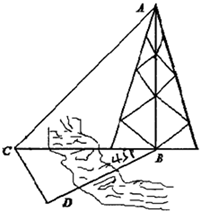如图，测量河对岸的塔的高度AB，可以选择与B在同一水平面内的两个点C、D．测得由C望A的仰角∠ACB=45°，方位角∠BCD═60°、∠BDC=75°，又测得C、D相距20米．试求塔的高度AB．
已知实数x、y满足x∈A，y∈B，
（1）若A={0，1，2}，B={0，1，2}，求x+yi为虚数的概率；
（2）若A=[0，1]，B=[0，1]，求x、y满足不等式组
y≥x2
y≤
x
的概率．
等比数列{an}的首项为a1，公比为q（q≠-1），用Sn→m表示这个数列的第n项到第m项共m-n+1项的和．
（Ⅰ）计算S1→3，S4→6，S7→9，并证明它们仍成等比数列；
（Ⅱ）受上面（Ⅰ）的启发，你能发现更一般的规律吗？写出你发现的一般规律，并证明．
已知等比数列{an}的前n项和为Sn=3n+a，n∈N*，则实数a的值是
 
．
如图是一个运行程序框图，则输出的S=（　　）
A、7B、11C、14D、25
已知复数z=a2-1+（a+1）i（a∈R）为纯虚数，则
.
z
为
 
．
为了调查某厂工人生产某种产品的能力，随机抽查了20位工人某天生产该产品的数量．产品数量的分组区间为[45，55），[55，65），[65，75），[75，85），[85，95），由此得到频率分布直方图，如右图．
估算众数，中位数，平均数．
已知x、y是正实数，且x+3y=1，求当x、y分别取何值时，
1
x
+
1
y
的值最小．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网