题目内容

20．在三角形ABC中，三个内角A，B，C所对的边分别为a，b，c，若acosA=bcosB，则三角形ABC一定是（　　）三角形．
A．直角B．等边C．钝角D．等腰或直角

分析 首先利用正弦定理求得sin2A=sin2B，进一步利用三角函数的诱导公式求出结果．

解答 解：已知：acosA=bcosB，
利用正弦定理：$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=2R$，
解得：sinAcosA=sinBcosB，
sin2A=sin2B，
所以：2A=2B或2A=180°-2B，
解得：A=B或A+B=90°，
所以：△ABC的形状一定是等腰或直角三角形．
故选：D．

点评 本题考查的知识要点：正弦定理的应用，三角函数的诱导公式的应用，考查了转化思想，属于基础题．

练习册系列答案
相关题目
10．如图是一个空间几何体的三视图，则该几何体体积是（　　）
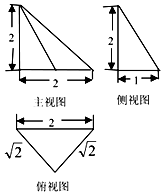
A．$\frac{1}{3}$B．1C．$\frac{4}{3}$D．$\frac{2}{3}$
11．已知△ABC中，内角A、B、C所对的边分别为a、b、c，若a2=b2+c2-bc，a=3，则△ABC的面积的最大值为（　　）
A．$2\sqrt{3}$B．9C．$\frac{{9\sqrt{3}}}{2}$D．$\frac{{9\sqrt{3}}}{4}$
8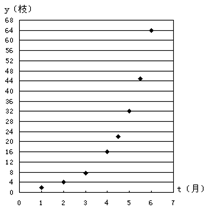．如图给出了红豆生长时间t（月）与枝数y（枝）的散点图：那么“红豆生南国，春来发几枝．”的红豆生长时间与枝数的关系用下列哪个函数模型拟合最好？（　　）
A．二次函数：y=2t2B．幂函数：y=t3
C．指数函数：y=2tD．对数函数：y=log2t
15．（1）已知tanα=2，求$\frac{sinα+cosα}{sinα-cosα}$的值
（2）化简：$\frac{sin（\frac{π}{2}+α）cos（\frac{5π}{2}-α）tan（-π+α）}{tan（7π-α）sin（π+α）}$．
5．已知f（x）是一次函数，且f（0）=1，f（1）=3，
（1）求函数f（x）的解析式．
（2）若g（x）=2f（x），且g（m2-2）＜g（m），求m的取值范围．
12．已知函数f（x）=x2+ax+4，若对任意的x∈（0，2]，f（x）≤6恒成立，则实数a的最大值为（　　）
A．-1B．1C．-2D．2
9．已知二次函数f（x）图象的对称轴是直线x=2，且f（0）=3，f（2）=1，若在[0，m]有最大值3，最小值1，则实数m的取值范围是（　　）
A．（0，+∞）B．[2，+∞）C．（0，2]D．[2，4]
10．集合A={x|x＜3}，B={x|x2-5x＜0}，则A∩B是（　　）
A．{x|0＜x＜3}B．{x|0＜x＜5}C．{x|3＜x＜5}D．{x|x＜0}

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网