题目内容
设数列{an}的前n项和为Sn,且Sn=n2-
,n∈N*.
(Ⅰ)证明:{a2n}是等差数列;
(Ⅱ)求数列{
}前n项和Tn.
| 1 |
| 4 |
(Ⅰ)证明:{a2n}是等差数列;
(Ⅱ)求数列{
| 1 |
| Sn |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)根据当n≥2时an=Sn-Sn-1,由2n≥2求出a2n的式子,由式子的特点判断出数列{a2n}是等差数列;
(2)由题意求出
,利用裂项相消法求出前n项和Tn.
(2)由题意求出
| 1 |
| Sn |
解答:
解:(1)当n=1时,a1=S1=1-
,a1=
,
当n≥2时,an=Sn-Sn-1=(n2-
)-[(n+1)2-
]=-2n-1,
又2n≥2,所以a2n=-4n-1,
所以数列{a2n}是以-5为首项,公差为-4的等差数列;
(2)由Sn=n2-
得,
=
=
=
-
,
所以Tn=(
-
)+(
-
)+…+(
-
)
=2-
=
.
| 1 |
| 4 |
| 3 |
| 4 |
当n≥2时,an=Sn-Sn-1=(n2-
| 1 |
| 4 |
| 1 |
| 4 |
又2n≥2,所以a2n=-4n-1,
所以数列{a2n}是以-5为首项,公差为-4的等差数列;
(2)由Sn=n2-
| 1 |
| 4 |
| 1 |
| Sn |
| 1 | ||
n2-
|
| 1 | ||||
(n+
|
| 1 | ||
n-
|
| 1 | ||
n+
|
所以Tn=(
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
|
| 1 | ||
n-
|
| 1 | ||
n+
|
=2-
| 1 | ||
n+
|
| 4n |
| 2n+1 |
点评:本题考查了an与Sn的关系式,等差数列的通项公式,裂项相消法求数列前n项和,属于中档题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知a∈R,i是虚数单位,复数z=a+i,若z2为纯虚数,则z=( )
| A、1+i |
| B、-1+i |
| C、1+i或-1+i |
| D、2i或-2i |
下列函数与y=x是相同函数的是( )
A、y=
| ||
B、y=(
| ||
| C、y=lnex | ||
| D、y=elnx |
若变量x,y满足约束条件
,则z=2x+y的最大值为( )
|
| A、1 | B、-1 | C、-2 | D、-4 |
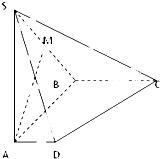 如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.
如图,在四棱锥S-ABCD中,侧棱SA⊥底面ABCD,AD∥BC,∠ABC=90°,SA=AB=BC=2,AD=1.M是棱SB的中点.