题目内容
集合A={α|α=
,n∈Z}∪{α|α=2nπ±
π,n∈Z},B={β|β=
,n∈Z}∪{β|β=nπ+
π,n∈Z},则A、B之间关系为( )
| nπ |
| 2 |
| 2 |
| 3 |
| 2nπ |
| 3 |
| 1 |
| 2 |
| A、B?A | B、A?B |
| C、B?A | D、A?B |
考点:集合的包含关系判断及应用
专题:计算题,集合
分析:分类讨论,化简集合A,B,即可得出结论.
解答:
解:α=
,n∈Z,(1)n=2k时,α=kπ;(2)n=2k+1时 α=kπ+
π,与β=nπ+
π等价;
β=
,n∈Z,(1)n=3m时,β=2mπ与α=kπ不等价;
(2)n=3m+1时,β=2mπ+
π与α=2nπ+
π等价;
(3)n=3m+2时,β=2mπ+
与α=2nπ-
等价.
综上:B?A.
故选:C.
| nπ |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
β=
| 2nπ |
| 3 |
(2)n=3m+1时,β=2mπ+
| 2 |
| 3 |
| 2 |
| 3 |
(3)n=3m+2时,β=2mπ+
| 4π |
| 3 |
| 2π |
| 3 |
综上:B?A.
故选:C.
点评:本题考查集合的包含关系判断及应用,考查分类讨论的数学思想,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
若函数f(x)满足:f(x)-4f(
)=x,则|f(x)|的最小值为( )
| 1 |
| x |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若实数(x,y)满足条件
,则z=
的最大值为( )
|
| x2+(y+1)2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、3 |
复数z=
(i为虚数单位)的共轭复数为( )
| 1+2i |
| i |
| A、2-i | B、2+i |
| C、-2+i | D、-2-i |
从1,2,3,4,5,6这六个数中,每次取出两个不同的数记为a,b,则共可得到2
的不同值的个数是( )
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
已知集合A={x|
≥0},集合B={y|y=sinx,x∈R},则B∩CRA=( )
| 1+x |
| 1-x |
| A、∅ | B、{1} |
| C、{-1} | D、{-1,1} |
在星期一至星期五的5天内安排语、数、英三科测试,每天最多进行一门考试,且语文和数学不能连续两天考试,那么不同的考试安排方案种数共有( )
| A、18 | B、36 | C、12 | D、48 |
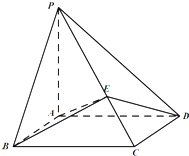 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为平行四边形,AB=1,BC=