题目内容
从1,2,3,4,5,6这六个数中,每次取出两个不同的数记为a,b,则共可得到2
的不同值的个数是( )
| b |
| a |
| A、20 | B、22 | C、24 | D、28 |
考点:组合及组合数公式
专题:排列组合
分析:从1,2,3,4,5,6这六个数中(两数在分子和分母不同),减去相同的数字即可得到答案.
解答:
解:从1,2,3,4,5,6这六个数中,每次取出两个不同的数排列有
=30,
因为:
=
=
,
=
=
,
=
,
=
,
=
,
=
,
所以每次取出两个不同的数记为a,b,则共可得到2
的不同值的个数是30-8=22种.
故选:B.
| A | 2 6 |
因为:
| 1 |
| 2 |
| 3 |
| 6 |
| 2 |
| 4 |
| 2 |
| 1 |
| 6 |
| 3 |
| 4 |
| 2 |
| 1 |
| 3 |
| 2 |
| 6 |
| 3 |
| 1 |
| 6 |
| 2 |
| 2 |
| 3 |
| 4 |
| 6 |
| 3 |
| 2 |
| 6 |
| 4 |
所以每次取出两个不同的数记为a,b,则共可得到2
| b |
| a |
故选:B.
点评:本题考查了排列、组合及简单的计数问题,解答的关键是想到把相等的数字去掉,属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下面是一个2×2列联表:
则表中a,b的值分别为( )
| y1 | y2 | 合计 | |
| x1 | a | c | 73 |
| x2 | 22 | 25 | 47 |
| 合计 | b | 46 | 120 |
| A、94,72 |
| B、52,50 |
| C、52,74 |
| D、74,52 |
已知函数f(x)=
,则f(f(-
))的值为( )
|
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
集合A={α|α=
,n∈Z}∪{α|α=2nπ±
π,n∈Z},B={β|β=
,n∈Z}∪{β|β=nπ+
π,n∈Z},则A、B之间关系为( )
| nπ |
| 2 |
| 2 |
| 3 |
| 2nπ |
| 3 |
| 1 |
| 2 |
| A、B?A | B、A?B |
| C、B?A | D、A?B |
质点做直线运动,其速度v(t)=3t2-2t+3,则它在第2秒内所走的路程为( )
| A、1 | B、3 | C、5 | D、7 |

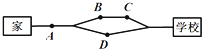 小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是
小明早上从家里出发到学校上课,如图所示,有两条路线可走,且走哪条路线的可能性是相同的,图中A、B、C、D处都有红绿灯,小明在每个红绿灯处遇到红灯的概率都是