题目内容
已知抛物线y2=16x的焦点为F,直线y=k(x-4)与此抛物线相交于P,Q两点,则
+
=( )
| 1 |
| |FP| |
| 1 |
| |FQ| |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点:抛物线的简单性质
专题:计算题,直线与圆,圆锥曲线的定义、性质与方程
分析:由抛物线y2=16x可得焦点F(4,0),因此直线y=k(x-4)过焦点.把直线方程与抛物线方程联立得到根与系数的关系,利用弦长公式即可得出.
解答:
解:由抛物线y2=16x可得焦点F(4,0),
因此直线y=k(x-4)过焦点.
设P(x1,y1),Q(x2,y2).,则|FP|=x1+4,|FQ|=x2+4.
联立
.化为k2x2-(16+8k2)x+16k2=0(k≠0).
∵△>0,∴x1+x2=
,x1x2=16.
∴
+
=
+
=
=
=
.
故选C.
因此直线y=k(x-4)过焦点.
设P(x1,y1),Q(x2,y2).,则|FP|=x1+4,|FQ|=x2+4.
联立
|
∵△>0,∴x1+x2=
| 16+8k2 |
| k2 |
∴
| 1 |
| |FP| |
| 1 |
| |FQ| |
| 1 |
| x1+4 |
| 1 |
| x2+4 |
| (x1+x2)+8 |
| x1x2+4(x1+x2)+16 |
| ||
32+4(8+
|
| 1 |
| 4 |
故选C.
点评:本题考查了抛物线的焦点弦问题,注意运用定义法解题,考查联立直线方程和抛物线方程,消去未知数,运用韦达定理和弦长公式,属于中档题.

练习册系列答案
相关题目
若{1,a,
}={0,a2,a+b},则a2013+b2012的值为( )
| b |
| a |
| A、0 | B、1 | C、±1 | D、-1 |
从分别写有A,B,C,D,E的五张卡片中任取两张,这两张的字母顺序恰好相邻的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
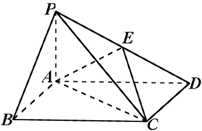 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=3,且三棱锥E-ACD的体积为1.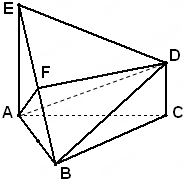 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证: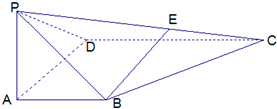
 如图所示,四棱锥P-ABCD的底面是直角梯形,PA⊥底面ABCD,AB⊥AD,CD⊥AD,CD=2AB,E为PC的中点,PA=AD=AB=1.
如图所示,四棱锥P-ABCD的底面是直角梯形,PA⊥底面ABCD,AB⊥AD,CD⊥AD,CD=2AB,E为PC的中点,PA=AD=AB=1.