题目内容
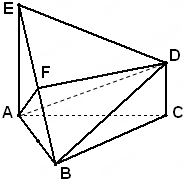 如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:
如图,已知△ABC是正三角形,EA、CD都垂直于平面ABC,且EA=AB=2a,DC=a,F是BE的中点,求证:(1)FD∥平面ABC;
(2)AF⊥平面EDB;
(3)求直线AD与平面EDB所成角的余弦值.
考点:直线与平面所成的角,直线与平面垂直的判定
专题:空间位置关系与距离,空间角
分析:(1)取AB的中点M,连FM,MC,只要证明FD∥MC即可;
(2)只要证明FD⊥AF,AF⊥EB,利用线面垂直的判定定理解答;
(3)由(2)可得AD在平面EBD的射影为DF,得到直线AD与平面EDB所成角为∠ADF.
(2)只要证明FD⊥AF,AF⊥EB,利用线面垂直的判定定理解答;
(3)由(2)可得AD在平面EBD的射影为DF,得到直线AD与平面EDB所成角为∠ADF.
解答:
(1)证明:取AB的中点M,连FM,MC,
∵F、M分别是BE、BA的中点,
∴FM∥EA,FM=
EA,
∵EA、CD都垂直于平面ABC,
∴CD∥EA,
∴CD∥FM,
又DC=a,∴FM=DC,
∴四边形FMCD是平行四边形,
∴FD∥MC,又FD?平面ABC,MC?平面ABC,
∴FD∥平面ABC;
(2)证明:∵M是AB的中点,△ABC是正三角形,
∴CM⊥AB,
又CM⊥AE,∴CM⊥面EAB,∴CM⊥AF,FD⊥AF,
因F是BE的中点,EA=AB,∴AF⊥EB,
FD∩BE=F,
∴AF⊥平面EDB.
(3)由(2)可得AD在平面EBD的射影为DF,所以直线AD与平面EDB所成角为∠ADF,AF=
a,AD=
a,DF=
a,cos∠ADF=
=
;
所以直线AD与平面EDB所成角的余弦值为
.
∵F、M分别是BE、BA的中点,
∴FM∥EA,FM=
| 1 |
| 2 |
∵EA、CD都垂直于平面ABC,
∴CD∥EA,
∴CD∥FM,
又DC=a,∴FM=DC,
∴四边形FMCD是平行四边形,
∴FD∥MC,又FD?平面ABC,MC?平面ABC,
∴FD∥平面ABC;
(2)证明:∵M是AB的中点,△ABC是正三角形,
∴CM⊥AB,
又CM⊥AE,∴CM⊥面EAB,∴CM⊥AF,FD⊥AF,
因F是BE的中点,EA=AB,∴AF⊥EB,
FD∩BE=F,
∴AF⊥平面EDB.
(3)由(2)可得AD在平面EBD的射影为DF,所以直线AD与平面EDB所成角为∠ADF,AF=
| 2 |
| 5 |
| 3 |
| DF |
| AD |
| ||
| 5 |
所以直线AD与平面EDB所成角的余弦值为
| ||
| 5 |
点评:本题考查了线面平行和线面垂直的判断以及线面角的求法,关键是将线面关系转化为线线关系解答.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若P={1,2},Q={1,a2},且P=Q,则a=( )
| A、2 | ||
| B、-2 | ||
C、±
| ||
D、
|
下列推理正确的是( )
| A、把a(b+c)与loga(x+y)类比,则有loga(x+y)=logax+logay |
| B、把a(b+c)与sin(x+y)类比,则有sin(x+y)=sinx+siny |
| C、把a(b+c)与ax+y类比,则有ax+y=ax+ay |
| D、把a(b+c)与a*(b+c)类比,则有a*(b+c)=a*b+a* |
已知抛物线y2=16x的焦点为F,直线y=k(x-4)与此抛物线相交于P,Q两点,则
+
=( )
| 1 |
| |FP| |
| 1 |
| |FQ| |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
已知x,y的取值如表所示,若y与x线性相关,且
=0.95x+a,则a=( )
 |
| y |
| x | 0 | 1 | 3 | 4 |
| y | 2.2 | 4.3 | 4.8 | 6.7 |
| A、2.2 | B、2.6 |
| C、2.8 | D、2.9 |
 数列{
数列{