题目内容
已知函数f(x)=
+lnx(a∈R).
(1)求f(x)的最小值;
(2)当a=2时,求证:ln(n+1)+2
>nln(2e)(n∈N*).
| a |
| x |
(1)求f(x)的最小值;
(2)当a=2时,求证:ln(n+1)+2
| n |
 |
| i+1 |
| i |
| i+1 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)先求出f′(x)=
,x>0,再讨论①a≤0时,②a>0时的情况,从而求出函数的最小值;
(2)a=2时,由(1)得f(x)≥ln2+1,从而lnx≥ln2+1-
=ln(2e)-
(*),分别令x=
,
…,
代入(*)得下列n个不等式,得ln
++ln
+…+ln
>nln(2e)-2(
+2×
+…+2×
),进而证明ln(n+1)+2
>nln(2e).
| x-a |
| x2 |
(2)a=2时,由(1)得f(x)≥ln2+1,从而lnx≥ln2+1-
| 2 |
| x |
| 2 |
| x |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
| n |
 |
| i=1 |
| i |
| i+1 |
解答:
解:(1)∵f′(x)=
,x>0,
①a≤0时,f′(x)≥0,f(x)在(0,+∞)上递增,
∴f(x)无最值,
②a>0时,
令f′(x)>0,解得:x>a,
令f′x)<0,解得:0<x<a,
∴f(x)在(0,a)递减,在(a,+∞)递增,
∴f(x)min=f(a)=lna+1,
综上,a≤0时,f(x)无最值,a>0时,f(x)min=f(a)=lna+1,
(2)a=2时,由(1)得f(x)≥ln2+1,
即
+lnx≥ln2+1,从而lnx≥ln2+1-
=ln(2e)-
(*),
∴分别令x=
,
…,
代入(*)得下列n个不等式,
ln
>ln(2e)-
=ln(2e)-2×
,
ln
>ln(2e)-
=ln(2e)-2×
,
…,
ln
>ln(2e)-(2×
),
将所述n个不等式相加得:
ln
++ln
+…+ln
>nln(2e)-2(
+2×
+…+2×
),
∴ln(n+1)>nln(2e)-2(
+
+…+
),
即ln(n+1)+2
>nln(2e).
| x-a |
| x2 |
①a≤0时,f′(x)≥0,f(x)在(0,+∞)上递增,
∴f(x)无最值,
②a>0时,
令f′(x)>0,解得:x>a,
令f′x)<0,解得:0<x<a,
∴f(x)在(0,a)递减,在(a,+∞)递增,
∴f(x)min=f(a)=lna+1,
综上,a≤0时,f(x)无最值,a>0时,f(x)min=f(a)=lna+1,
(2)a=2时,由(1)得f(x)≥ln2+1,
即
| 2 |
| x |
| 2 |
| x |
| 2 |
| x |
∴分别令x=
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
ln
| 2 |
| 1 |
| 2 | ||
|
| 1 |
| 2 |
ln
| 3 |
| 2 |
| 2 | ||
|
| 2 |
| 3 |
…,
ln
| n+1 |
| n |
| n |
| n+1 |
将所述n个不等式相加得:
ln
| 2 |
| 1 |
| 3 |
| 2 |
| n+1 |
| n |
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
∴ln(n+1)>nln(2e)-2(
| 1 |
| 2 |
| 2 |
| 3 |
| n |
| n+1 |
即ln(n+1)+2
| n |
 |
| i=1 |
| i |
| i+1 |
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,不等式的证明,是一道综合题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
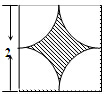 如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )
如图所示,墙上挂有边长为2的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为1的圆孤,某人向此板投镖,假设每次都能击中木板,且击中木板上每个点的可能性都一样,则它击中阴影部分的概率是( )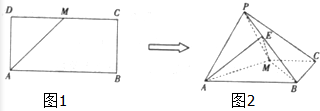 如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=
如图,已知长方形ABCD中,AB=2,AD=1,M为DC的中点.将△ADM沿AM折起到△APM,使得平面APM⊥平面ABCM,点E在线段PB上,且PE=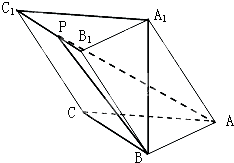 在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
在三棱柱ABC-A1B1C1中,已知AB=BC=2,∠ABC=90°,点A1在底面ABC的投影为B,且A1B=2
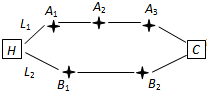 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为