题目内容
已知函数f(x)=lnx+
,a为常数,若a=
,求函数f(x)在(1,e)上的值域.
| a |
| x+1 |
| 9 |
| 2 |
考点:函数的值域
专题:函数的性质及应用
分析:对函数解析式求导,判断导函数在区间上的正负,进而判断出函数的单调新,求得函数的最大和最小值.
解答:
解:f′(x)=
-
=
=
,
∵x∈(1,e),
∴当1<x<2时f′(x)<0,函数f(x)单调减,
当2<x<e时,f′(x)>0,函数f(x)单调增,
故x=2时,f′(x)=0,函数f(x)取最小值,f(2)=ln2+
,
f(1)=ln1+
=
,f(e)=lne+
,f(e)<f(1),
∴函数的最大值为
,
故函数f(x)在(1,e)上的值域为[ln2+
,
).
| 1 |
| x |
| ||
| (x+1)2 |
x2+2x+1-
| ||
| x(x+1)2 |
(x-
| ||||
| x(x+1)2 |
∵x∈(1,e),
∴当1<x<2时f′(x)<0,函数f(x)单调减,
当2<x<e时,f′(x)>0,函数f(x)单调增,
故x=2时,f′(x)=0,函数f(x)取最小值,f(2)=ln2+
| 3 |
| 2 |
f(1)=ln1+
| 9 |
| 4 |
| 9 |
| 4 |
| ||
| e+1 |
∴函数的最大值为
| 9 |
| 4 |
故函数f(x)在(1,e)上的值域为[ln2+
| 3 |
| 2 |
| 9 |
| 4 |
点评:本题主要考查了导函数的应用.在判断函数单调性的问题上,对函数求导进行判断是常用方法,应熟练应用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目

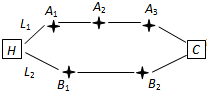 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为