题目内容
α,β∈(0,
),cos(2α-β)=
,sin(α-2β)=-
,则cos(α+β)的值等于 .
| π |
| 4 |
| ||
| 2 |
| 1 |
| 2 |
考点:两角和与差的余弦函数
专题:三角函数的求值
分析:根据已知条件列出关于α和β的方程组求得α和β,最后代入cos(α+β)即可.
解答:
解:∵α,β∈(0,
),
∴2α-β∈(-
,
),α-2β∈(-
,
)
∵cos(2α-β)=
,sin(α-2β)=-
,
∴
或
求得α=β=
或α=-
,β=
(舍),
∴cos(α+β)=cos
=
,
故答案为:
| π |
| 4 |
∴2α-β∈(-
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 4 |
∵cos(2α-β)=
| ||
| 2 |
| 1 |
| 2 |
∴
|
|
| π |
| 6 |
| π |
| 18 |
| π |
| 18 |
∴cos(α+β)=cos
| π |
| 3 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查了特殊三角函数值的应用.也可以采用两角和与差的余弦函数公式求得答案.

练习册系列答案
相关题目
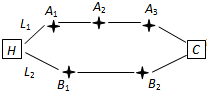 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为