题目内容
在极坐标系中,直线ρ(cosθ-sinθ)=1与直线ρcosθ=1的夹角大小为 .
考点:简单曲线的极坐标方程
专题:坐标系和参数方程
分析:把极坐标方程化为直角坐标方程,分别求出它们的斜率,可得它们的夹角.
解答:
解:直线ρ(cosθ-sinθ)=1即 x-y-1=0,斜率为1;
直线ρcosθ=1即 x=1,斜率不存在,故这两条直线的夹角为
,
故答案为:
.
直线ρcosθ=1即 x=1,斜率不存在,故这两条直线的夹角为
| π |
| 4 |
故答案为:
| π |
| 4 |
点评:本题主要考查把极坐标方程化为直角坐标方程的方法,求两条直线的夹角,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
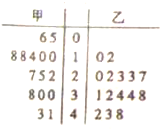 从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为
从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|

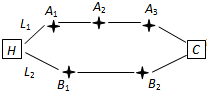 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为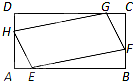 如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为
如图,已知矩形ABCD,AB=2,AD=1.若点E,F,G,H分别在线段AB,BC,CD,DA上,且AE=BF=CG=DH,则四边形EFGH面积的最小值为