题目内容
已知三棱锥P-ABC的所有顶点都在球O的球面上,PC为球O的直径,且PC⊥OA,PC⊥OB,△OAB为等边三角形,三棱锥P-ABC的体积为
,则球O的半径为 .
4
| ||
| 3 |
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:欲求球的半径r.利用截面的性质即可得到三棱锥P-ABC的体积可看成是两个小三棱锥P-ABO和C-ABO的体积和,即可计算出三棱锥的体积,从而建立关于r的方程,即可求出r,从而解决问题.
解答:
解:设球心为O,球的半径r.
∵PC⊥OA,PC⊥OB,∴PC⊥平面AOB,
三棱锥P-ABC的体积可看成是两个小三棱锥P-ABO和C-ABO的体积和.
∴V三棱锥P-ABC=V三棱锥P-ABO+V三棱锥C-ABO=
×
×r2×r×2=
,
∴r=2.
故答案为:2.
∵PC⊥OA,PC⊥OB,∴PC⊥平面AOB,
三棱锥P-ABC的体积可看成是两个小三棱锥P-ABO和C-ABO的体积和.
∴V三棱锥P-ABC=V三棱锥P-ABO+V三棱锥C-ABO=
| 1 |
| 3 |
| ||
| 4 |
4
| ||
| 3 |
∴r=2.
故答案为:2.
点评:本题考查棱锥的体积,考查球内接多面体,解题的关键是确定三棱锥P-ABC的体积可看成是两个小三棱锥P-ABO和C-ABO的体积和.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
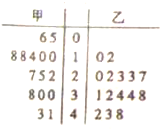 从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为
从甲乙两个城市分别随机抽取15台自动售货机,对其销售额进行统计,统计数据用茎叶图表示(如图所示),设甲乙两组数据的平均数分别为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}是等差数列,a1+a3+a5=105,a2+a4+a6=99,{an}的前n项和为Sn,则使得Sn达到最大的n是( )
| A、18 | B、19 | C、20 | D、21 |
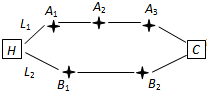 家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为
家住H小区的王先生开车到C单位上班有L1、L2两条路线(如图),其中路线L1上有A1、A2、A3三个路口,各路口遇到红灯的概率均为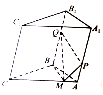 如图,在三棱柱ABC-A1B1C1的侧棱A1A和B1B上各有一个动点P,Q,且满足A1P=BQ,M是棱CA上的动点,则
如图,在三棱柱ABC-A1B1C1的侧棱A1A和B1B上各有一个动点P,Q,且满足A1P=BQ,M是棱CA上的动点,则