题目内容
已知a≥0，b≥0，c≥0，求证：
+
≥a+b+c．
| a2+ab+b2 |
| b2+bc+c2 |
考点：不等式的证明
专题：证明题,推理和证明
分析：利用a2+ab+b2=(a+
)2+
≥(a+
)2，可知
≥a+
；同理可得
≥c+
；于是可证结论．
| b |
| 2 |
| b2 |
| 4 |
| b |
| 2 |
| a2+ab+b2 |
| b |
| 2 |
| b2+bc+c2 |
| b |
| 2 |
解答：
证明：∵a≥0，b≥0，c≥0，
a2+ab+b2=(a+
)2+
≥(a+
)2，
∴
≥a+
；
同理可得，
≥c+
；
∴
+
≥a+b+c．
a2+ab+b2=(a+
| b |
| 2 |
| b2 |
| 4 |
| b |
| 2 |
∴
| a2+ab+b2 |
| b |
| 2 |
同理可得，
| b2+bc+c2 |
| b |
| 2 |
∴
| a2+ab+b2 |
| b2+bc+c2 |
点评：本题考查不等式的证明，考查配方法与放缩法的综合应用，考查转化思想与推理论证能力，属于中档题．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
设集合A={0，a}，B={x∈Z||x|＜2 }，则“a=1”是“A⊆B”的（ ）
| A、充要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
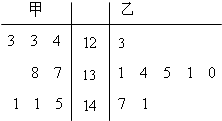为了解某校高一学生的中考数学成绩，分别从甲乙两班随机各抽取8名学生的中考数学成绩，获得如图所示的茎叶图．
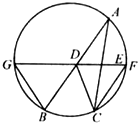如图，D，E分别为△ABC边AB，AC的中点，直线DE交于△ABC的外接圆于F，G两点，若BC=2EF，证明：