题目内容
6.过抛物线y=x2的焦点F作直线交抛物线于P,Q,若线段PF与QF的长度分别为m,n,则2m+n的最小值为( )| A. | $\frac{3}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{3+2\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
分析 设PQ的斜率k=0,因抛物线焦点坐标为(0,$\frac{1}{4}$),把直线方程y=$\frac{1}{4}$代入抛物线方程得m,n的值,可得$\frac{1}{m}$+$\frac{1}{n}$=4,利用“1”的代换,即可得到答案.
解答 解:抛物线y=4x2的焦点F为(0,$\frac{1}{4}$),
设PQ的斜率k=0,
∴直线PQ的方程为y=$\frac{1}{4}$,
代入抛物线y=x2得:x=±$\frac{1}{2}$,
即m=n=$\frac{1}{2}$,
∴$\frac{1}{m}$+$\frac{1}{n}$=4,
∴2m+n=$\frac{1}{4}$(2m+n)($\frac{1}{m}$+$\frac{1}{n}$)=$\frac{1}{4}$(3+$\frac{2m}{n}$+$\frac{n}{m}$)≥$\frac{3+2\sqrt{2}}{4}$
故选:C.
点评 本题考查抛物线的定义、标准方程,以及简单性质的应用,设k=0,求出m,n是解题的关键,属于中档题.

练习册系列答案
相关题目
16.将八进制数26(8)转化为十进制数,结果是( )
| A. | 20 | B. | 22 | C. | 24 | D. | 26 |
18.命题“?x0∈R,x0+1<0或${x_0}^2-{x_0}>0$”的否定形式是( )
| A. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | B. | ?x0∈R,x0+1≥0或${x_0}^2-{x_0}≤0$ | ||
| C. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ | D. | ?x0∈R,x0+1≥0且${x_0}^2-{x_0}≤0$ |
15.如图,某地一天中6时至14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b(其中A>0,ω>0,-π<φ<π),那么中午12时温度的近似值(精确到1°C)是( )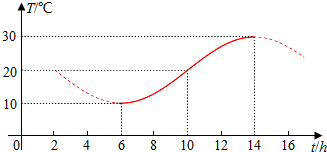

| A. | 25°C | B. | 26°C | C. | 27°C | D. | 28°C |
16.已知单调函数f(x)满足f(0)=3,且f(f(x)-ex-x)=e2+4,则函数零点所在区间为( )
| A. | (-4,-3) | B. | (-3,-2) | C. | (-2,-1) | D. | (-1,0) |