题目内容
若(2x-1)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),则
=( )
| a0 |
| a1+2a2+3a3+…+2014a2014 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
考点:二项式定理的应用
专题:二项式定理
分析:设f(x)=(2x-1)2014,对函数求导,令x=1,求出a1+2a2+3a3+…+2014•a2014的值,再求出a0的值即可得出结论.
解答:
解:设f(x)=(2x-1)2014=a0+a1x+a2x2+…+a2014x2014(x∈R),
∴f′(x)=2014•(2x-1)2013•2=a1+2a2x+3a3x2+…+2014•a2014x2013;
∴f′(1)=2014•1•2=a1+2a2+3a3+…+2014•a2014=2×2014;
又∵a0=(-1)2014=1,
∴
=
=
.
故选:C.
∴f′(x)=2014•(2x-1)2013•2=a1+2a2x+3a3x2+…+2014•a2014x2013;
∴f′(1)=2014•1•2=a1+2a2+3a3+…+2014•a2014=2×2014;
又∵a0=(-1)2014=1,
∴
| a0 |
| a1+2a2+3a3+…+2014a2014 |
| 1 |
| 2×2014 |
| 1 |
| 4028 |
故选:C.
点评:本题考查了二项式定理的应用问题,也考查了解决该类问题的常用方法--赋值法,正确赋值是迅速解答本题的关键.

练习册系列答案
相关题目
函数f(x)=
在[2,+∞)上( )
| 1 |
| x |
| A、有最大值无最小值 |
| B、有最小值无最大值 |
| C、有最大值和最小值 |
| D、无最大值和最小值 |
已知过点A(a,4)和B(-2,a)的直线与直线2x+y-1=0垂直,则a的值为( )
| A、0 | B、-8 | C、2 | D、10 |
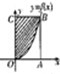 如图,长方形四个顶点为O(0,0),A(
如图,长方形四个顶点为O(0,0),A(