题目内容
当1＜x≤2时，不等式x2-2ax+a＜0恒成立，求实数a的取值范围．
考点：函数恒成立问题
专题：不等式的解法及应用
分析：构造将二次函数f（x）=x2-2ax+a，利用二次函数的图象和性质求解，要使不等式f（x）＜0恒成立，则只需求出函数在x∈（1，2]时的最大值即可．
解答：
解：令f（x）=x2-2ax+a，
则由二次函数的图象和性质可知，
当1＜x≤2时，不等式x2-2ax+a＜0恒成立等价于，
，
即
，
解得，a＞
，
∴实数a的取值范围(
，+∞)．
则由二次函数的图象和性质可知，
当1＜x≤2时，不等式x2-2ax+a＜0恒成立等价于，
|
即
|
解得，a＞
| 4 |
| 3 |
∴实数a的取值范围(
| 4 |
| 3 |
点评：本题主要考查二次函数的图象和性质在研究一元二次不等式中的应用，属于中档题．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
下列说法一定正确的是（ ）
| A、直角三角形绕其一边旋转形成圆锥 |
| B、等边三角形绕其一边旋转形成圆锥 |
| C、平面截圆锥所得的图形是圆 |
| D、过圆锥顶点的截面图形是等腰三角形 |
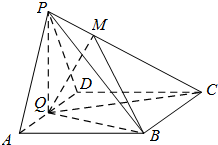如图在四棱锥P-ABCD中，底面ABCD是菱形，∠BAD=60°，平面PAD⊥平面ABCD，PA=PD=AD=2，Q为AD的中点，M是棱PC上一点，且PM=
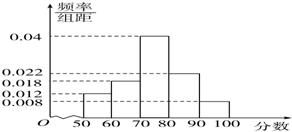某市的教育研究机构对全市高三学生进行综合素质测试，随机抽取了部分学生的成绩，得到如图所示的成绩频率分布直方图．