题目内容
已知椭圆C1:
+y2=1.
(Ⅰ)我们知道圆具有性质:若E为圆O:x2+y2=r2(r>0)的弦AB的中点,则直线AB的斜率kAB与直线OE的斜率kOE的乘积kAB•kOE为定值.类比圆的这个性质,写出椭圆C1的类似性质,并加以证明;
(Ⅱ)如图(1),点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值;
(Ⅲ)如图(2),过椭圆C2:
+
=1上任意一点P作C1的两条切线PM和PN,切点分别为M,N.当点P在椭圆C2上运动时,是否存在定圆恒与直线MN相切?若存在,求出圆的方程;若不存在,请说明理由.
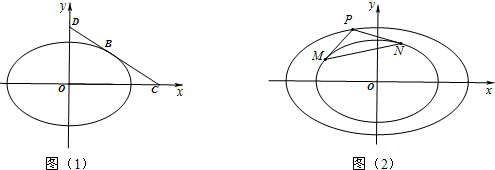
| x2 |
| 2 |
(Ⅰ)我们知道圆具有性质:若E为圆O:x2+y2=r2(r>0)的弦AB的中点,则直线AB的斜率kAB与直线OE的斜率kOE的乘积kAB•kOE为定值.类比圆的这个性质,写出椭圆C1的类似性质,并加以证明;
(Ⅱ)如图(1),点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,求三角形OCD面积的最小值;
(Ⅲ)如图(2),过椭圆C2:
| x2 |
| 8 |
| y2 |
| 2 |
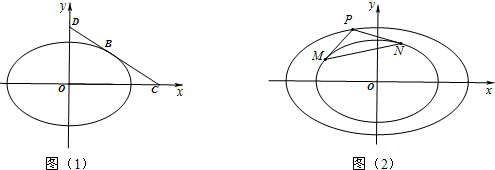
考点:直线与圆锥曲线的关系,函数与方程的综合运用
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设出A,B两点的坐标,由点差法得到
+(y1+y2)(y1-y2)=0,转化为过A,B两点直线的斜率及原点与AB中点连线的斜率得答案;
(Ⅱ)结合(Ⅰ)中的结论得到过椭圆上的B的切线的斜率,写出过点B的切线方程,求出切线在两坐标轴上的截距,代入三角形的面积公式,再由B点在椭圆上借助于基本不等式求出三角形OCD的面积的最小值;
(Ⅲ)设出P(m,n),写出椭圆在点M(x3,y3)处的切线方程,代入P点的坐标,即可说明点M(x3,y3)在直线
m+yn=1上,同理说明点N(x4,y4)在直线
m+yn=1上,由此得到直线MN的方程,求得原点到MN的距离为定值说明存在定圆恒与直线MN相切.
| (x1-x2)(x1+x2) |
| 2 |
(Ⅱ)结合(Ⅰ)中的结论得到过椭圆上的B的切线的斜率,写出过点B的切线方程,求出切线在两坐标轴上的截距,代入三角形的面积公式,再由B点在椭圆上借助于基本不等式求出三角形OCD的面积的最小值;
(Ⅲ)设出P(m,n),写出椭圆在点M(x3,y3)处的切线方程,代入P点的坐标,即可说明点M(x3,y3)在直线
| x |
| 2 |
| x |
| 2 |
解答:
解:(Ⅰ)若A,B为椭圆C1:
+y2=1上相异的两点,E(x0,y0)为A,B中点,
则直线AB的斜率kAB与直线OP的斜率kOE的乘积kOE•kAB必为定值;
证明:设A(x1,y1),B(x2,y2),则
,
两式作差得:
+(y1+y2)(y1-y2)=0,
∵仅考虑斜率存在的情况,
∴x0+2y0•kAB=0,即kOE•kAB=-
;
(Ⅱ)如图,
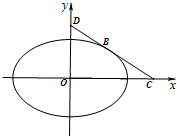
当点A无限趋近于点B时,割线AB的斜率就等于椭圆上的B的切线的斜率k,即k•kOB=-
,k=-
.
∴点B处的切线QB:y-y2=-
(x-x2),即
x+y2y=1,
令x=0,yD=
,令y=0,xC=
,
∴S△OCD=
×
=
.
又点B在椭圆的第一象限上,
∴x2>0,y2>0,
+y22=1,
∴1=
+y22≥2
=
x2y2,
∴S△OCD=
=
,当且仅当
=y22,即x2=
y2=1时取最小值.
∴当B(1,
)时,三角形OCD的面积的最小值为
;
(Ⅲ)设P(m,n),由(Ⅱ)知点M(x3,y3)处的切线为:
x+y3y=1.
又PM过点P(m,n),
∴
m+y3n=1,又可理解为点M(x3,y3)在直线
m+yn=1上.
同理点N(x4,y4)在直线
m+yn=1上,
∴直线MN的方程为:
x+ny=1.
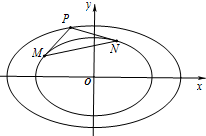
∴原点O到直线MN的距离d=
=
,
∴直线MN始终与圆x2+y2=
相切.
| x2 |
| 2 |
则直线AB的斜率kAB与直线OP的斜率kOE的乘积kOE•kAB必为定值;
证明:设A(x1,y1),B(x2,y2),则
|
两式作差得:
| (x1-x2)(x1+x2) |
| 2 |
∵仅考虑斜率存在的情况,
∴x0+2y0•kAB=0,即kOE•kAB=-
| 1 |
| 2 |
(Ⅱ)如图,

当点A无限趋近于点B时,割线AB的斜率就等于椭圆上的B的切线的斜率k,即k•kOB=-
| 1 |
| 2 |
| x2 |
| 2y2 |
∴点B处的切线QB:y-y2=-
| x2 |
| 2y2 |
| x2 |
| 2 |
令x=0,yD=
| 1 |
| y2 |
| 2 |
| x2 |
∴S△OCD=
| 1 |
| 2 |
| 2 |
| x2y2 |
| 1 |
| x2y2 |
又点B在椭圆的第一象限上,
∴x2>0,y2>0,
| x22 |
| 2 |
∴1=
| x22 |
| 2 |
|
| 2 |
∴S△OCD=
| 1 |
| x2y2 |
| ||
| 2 |
| x22 |
| 2 |
| 2 |
∴当B(1,
| ||
| 2 |
| 2 |
(Ⅲ)设P(m,n),由(Ⅱ)知点M(x3,y3)处的切线为:
| x3 |
| 2 |
又PM过点P(m,n),
∴
| x3 |
| 2 |
| x |
| 2 |
同理点N(x4,y4)在直线
| x |
| 2 |
∴直线MN的方程为:
| m |
| 2 |

∴原点O到直线MN的距离d=
| 1 | ||||
|
| ||
| 2 |
∴直线MN始终与圆x2+y2=
| 1 |
| 2 |
点评:本题主要考查直线、圆、椭圆等基础知识,考查类比推理论证能力、运算求解能力,考查一般到特殊的思想方法、函数与方程思想、数形结合思想、化归与转化思想.考查数学综合分析问题的能力以及创新能力,是压轴题.

练习册系列答案
相关题目
| ∫ | 2π 0 |
| A、0 | B、2 | C、4 | D、2π |
设集合A={x|x2-3x-4>0},B={x|-2≤x≤3},则(∁RA)∩B=( )
| A、R |
| B、[-2,-1] |
| C、[-1,3] |
| D、[-2,4] |
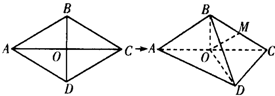 如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3
如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3