题目内容
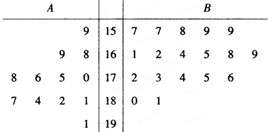 某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.
某园艺师培育了两种珍稀树苗A与B,株数分别为12与18,现将这30株树苗的高度编写成茎叶图如图(单位:cm)若树高在175cm以上(包括175cm)定义为“生长良好”,树高在175cm以下(不包括175cm)定义为“非生长良好”,且只有“B生长良好”的才可以出售.(Ⅰ)如果用分层抽样的方法从“生长良好”和“非生长良好”中抽取5株,再从这5株中选2株,那么至少有一株“生长良好”的概率是多少?
(Ⅱ)若从所有“生长良好”中选3株,用X表示所选中的树苗中能出售的株数,试写出X的分布列,并求X的数学期望.
考点:离散型随机变量的期望与方差,茎叶图
专题:概率与统计
分析:(1)结合排列组合知识求解,(2)先求出随机变量X的值,再分别求出概率,得出分布列,运用数学期望的公式求解.
解答:
解:(Ⅰ)根据茎叶图知,“生长良好”的有12株,“非生长良好”的有18株.
用分层抽样的方法抽取,每株被抽中的概率是
=
,
“生长良好”的有12×
=2株,“非生长良好”的有18×
=3株.
用事件A表示“至少有一株‘生长良好’的被选中”,
则P(A)=1-
=1-
=
,
因此从5株树苗中选2株,至少有一株“生长良好”的概率是
,
(Ⅱ)依题意,一共有12株生长良好,其中A种树苗有8株,B种树苗有4株,则X的所有可能取值为0,1,2,3,
P(X=0)=
=
;P(X=1)=
=
;P(X=2)=
=
;P(X=3)=
=
.
因此X的分布列如下:
所以X的数学期望:0×
+1×
+2×
+3×
=1
用分层抽样的方法抽取,每株被抽中的概率是
| 5 |
| 30 |
| 1 |
| 6 |
“生长良好”的有12×
| 1 |
| 6 |
| 1 |
| 6 |
用事件A表示“至少有一株‘生长良好’的被选中”,
则P(A)=1-
| ||
|
| 3 |
| 10 |
| 7 |
| 10 |
因此从5株树苗中选2株,至少有一株“生长良好”的概率是
| 7 |
| 10 |
(Ⅱ)依题意,一共有12株生长良好,其中A种树苗有8株,B种树苗有4株,则X的所有可能取值为0,1,2,3,
P(X=0)=
| ||
|
| 14 |
| 55 |
| ||||
|
| 28 |
| 55 |
| ||||
|
| 12 |
| 55 |
| ||
|
| 1 |
| 55 |
因此X的分布列如下:
| X | 0 | 1 | 2 | 3 | ||||||||
| P |
|
|
|
|
| 14 |
| 55 |
| 28 |
| 55 |
| 12 |
| 55 |
| 1 |
| 55 |
点评:本考查了实际问题和概率问题,统计知识与古典概率的求解,属于难题.

练习册系列答案
相关题目
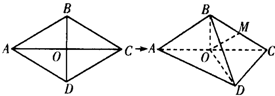 如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3
如图,平面四边形ABCD中,AB=BC=CD=DA=BD=6,O为AC,BD的交点.将四边形ABCD沿对角线AC折起,得到三棱锥B-ACD,且BD=3 如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若
如图,△ABC中,延长CB到D,使BD=BC,当E点在线段AD上移动时,若