题目内容
1.双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1的离心率e=$\frac{\sqrt{6}}{2}$.分析 由双曲线的方程可知:焦点在x轴上,a=2,b=$\sqrt{2}$,则c2=a2+b2=4+2=6,则c=$\sqrt{6}$,根据离心率公式可知:e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$,双曲线的离心率.
解答 解:由题意可知:双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{2}$=1,焦点在x轴上,a=2,b=$\sqrt{2}$,
则c2=a2+b2=4+2=6,则c=$\sqrt{6}$,
由双曲线的离心率公式可知:e=$\frac{c}{a}$=$\frac{\sqrt{6}}{2}$,
故答案为:$\frac{\sqrt{6}}{2}$.
点评 本题考查双曲线的标准方程及简单几何性质,考查双曲线的离心率公式,考查计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.一船以22$\sqrt{6}$ km/h的速度向正北航行,在A处看灯塔S在船的北偏东45°,1小时30分后航行到B处,在B处看灯塔S在船的南偏东15°,则灯塔S与B之间的距离为( )
| A. | 66 km | B. | 96 km | C. | 132 km | D. | 33 km |
9.设$a=ln3,b={log_2}\sqrt{3},c={log_3}\sqrt{2}$,则( )
| A. | a>b>c | B. | a>c>b | C. | b>a>c | D. | b>c>a |
16.已知函数f(x)=(1-cosx)sinx,则( )
| A. | f(x)是奇函数 | B. | f(x)是偶函数 | ||
| C. | f(x)既是奇函数也是偶函数 | D. | f(x)既不是奇函数也不是偶函数 |
6.若m、n为两条不重合的直线,α、β为两个不重合的平面,则下列命题中正确的是( )
| A. | 若m、n都平行于平面α,则m、n一定不是相交直线 | |
| B. | 若m、n都垂直于平面α,则m、n一定是平行直线 | |
| C. | 已知α、β互相平行,m、n互相平行,若m∥α,则n∥β | |
| D. | 若m、n在平面α内的射影互相平行,则m、n互相平行 |
13.下列函数中,是奇函数,又在定义域内为减函数的是( )
| A. | $y={({\frac{1}{2}})^x}$ | B. | $y=\frac{2}{x}$ | C. | y=-2x3 | D. | $y={log_2}{x^2}$ |
10.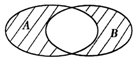 设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )
设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )
 设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )
设函数f(x)=lg(1-x2),集合A为函数f(x)的定义域,集合B=(-∞,0]则图中阴影部分表示的集合为( )| A. | [-1,0] | B. | (-1,0) | C. | (-∞,-1)∪[0,1) | D. | (-∞,-1]∪(0,1) |